Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

Лейбниц в письме де Боссу [355]в 1706 году. Цитируется по: Guicciardini, Reading the Principia, 159.

Например, нестандартный анализ Абрахама Робинсона, где рассматриваются гипердействительные числа. Прим. пер .

Термин «дифференциал» образован от латинского слова differentia – «разность». Прим. пер .

Лейбниц в письме де Боссу в 1706 году. Цитируется по: Guicciardini, Reading the Principia, 166.

Edwards, The Historical Development, 259.

Цитируется Edwards, The Historical Development, 259.

В этой записи смешиваются два разных x – тот x , что в левой части, совпадает с верхним пределом интегрирования в правой, но вот под знаком интеграла и в дифференциале – на деле другой. Фактически этот второй «немой», поскольку интегрировать можно по любой переменной. Чтобы не путаться, лучше использовать другую переменную интегрирования, так что этот интеграл может быть записан, например, как 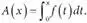Прим. пер .

Буква S от лат. summa «сумма». Прим. пер .

Edwards, The Historical Development, 236–38. На самом деле Лейбница интересовала сумма величин, обратных треугольным числам, которая вдвое больше суммы, рассмотренной в тексте книги. Смотрите также Grattan-Guinness, From the Calculus, 60–62.

Отсылка к английской поговорке о скрытой цели, восходящей к «Гамлету». Полоний комментирует поведение Гамлета: «Хоть это и безумие, но в нем есть метод» (акт 2, сцена 2). Прим. пер .

Из письма Эренфриду Вальтеру фон Чирнхаусу [356]в 1679 году. Цитируется по Guicciardini, Reading the Principia, 145.

Статистику для ВИЧ и СПИД смотрите на сайте https://ourworldindata.org/hiv-aids/. Историю вируса и попыток с ним бороться смотрите на сайте https://www.avert.org/professionals/history-hiv-aids/overview.

Оппортунистические инфекции – это заболевания, которыми люди со здоровой иммунной системой обычно не болеют. Прим. пер .

The Stages of HIV Infection, AIDSinfo, https://aidsinfo.nih.gov/understanding-hiv-aids/fact-sheets/19/46/the-stages-of-hiv-infection.

Ho et al., Rapid Turnover; Perelson et al., HIV-1 Dynamics; Perelson, Modelling Viral and Immune System; и Murray, Mathematical Biology 1.

Результаты вероятностных расчетов впервые появились в работе: Perelson et al., Dynamics of HIV-1.

Gorman, Dr. David Ho.

Американское математическое общество, премия Макса Дельбрюка 2017 года в биологической физике, https://www.aps.org/programs/honors/prizes/prizerecipient.cfm?first_nm=Alan&last_nm=Perelson&year=2017.

Multidisciplinary Team Aids Understanding of Hepatitis C Virus and Possible Cure, Los Alamos National Laboratory, March 2013, http://www.lanl.gov/discover/publications/connections/2013–03/understanding-hep-c.php. Введение в математическое моделирование гепатита С смотрите в работе: Perelson and Guedj, Modelling Hepatitis C.

Из слов автора может сложиться впечатление, что многоклеточные организмы появились после кембрийского взрыва. Это не так – они встречались и в докембрии. Прим. пер .

О многих направлениях, отпочковавшихся от анализа с 1700-х до нашего времени, смотрите Kline, Mathematics in Western Culture; Boyer, The History of the Calculus; Edwards, The Historical Development; Grattan-Guinness, From the Calculus; Katz, History of Mathematics; Dunham, The Calculus Gallery; Stewart, In Pursuit of the Unknown; Higham et al., The Princeton Companion; и Goriely, Applied Mathematics.

Опцион – вид сделки, когда покупатель (продавец) получает право купить (продать) некий актив в будущем по заранее установленной цене. Прим. пер .

Peterson, Newton’s Clock; Guicciardini, Reading the Principia; Stewart, In Pursuit of the Unknown; и Stewart, Calculating the Cosmos.

Kline, Mathematics in Western Culture, 234– 86, о значительном влиянии, которое труды Ньютона оказали на ход западной философии, религии, эстетики и литературы, а также на науку и математику. Смотрите также W. Bristow, Enlightenment, https://plato.stanford.edu/entries/enlightenment/.

D. Brewster, Memoirs of the Life, Writings, and Discoveries of Sir Isaac Newton, том 2 (Edinburgh: Thomas Constable, 1855), 158.

Об удивительной истории этого яблока смотрите Gleick, Isaac Newton, 55–57, и примечание 18 на стр. 207. Смотрите также Martínez, Science Secrets, глава 3.

Черновик письма Ньютона Пьеру де Майзо, написанный в 1718 году; доступен в интернете по адресу: https://cudl.lib.cam.ac.uk/view/MS-ADD-03968/1349в собрании Библиотеки Кембриджского университета.

Ньютон не открывал закон обратных квадратов. Впервые идею, что движение планет может обеспечить сила притяжения, обратно пропорциональная квадрату расстояния, высказал в 1645 году французский астроном Исмаэль Буйо. Затем к ней приходили и другие ученые. Роберт Гук в 1679 году в явном виде сформулировал этот закон в письме к Ньютону и попросил математически обосновать его (что Ньютон и сделал). Однако Ньютон оспаривал приоритет Гука, ссылаясь на работы Буйо и Борелли, а также обсуждение этой идеи с Кристофером Реном еще до письма Гука. Ученый утверждал, что даже если бы впервые услышал об этом законе от Гука, то у него были некоторые права на него, потому что, в отличие от Гука, он его доказал: «Без моих демонстраций, с которыми господин Гук еще не знаком, никакой рассудительный философ не может поверить в его точность». Более того, по словам Ньютона, он знал об этом законе и раньше. Однако доказательств этому нет. В записях ученого 1669 года есть утверждение, что в случае кругового планетного движения «стремление отступить» (что позднее назовут центробежной силой) обратно пропорционально квадрату расстояния до центра, однако это не совсем то (хотя идеологически близко), и на язык центростремительной силы Ньютон перешел только после переписки с Гуком в 1679–1680 годах. Тем не менее эти записи показывают, что какие-то основания оспаривать приоритет Гука у Ньютона были. Специалисты продолжают спорить, что именно Ньютон позаимствовал у Гука (значительная часть личных бумаг Гука уничтожена или исчезла). Прим. пер .

Asimov, Asimov’s Biographical Encyclopedia, 138, дает одну из версий этой известной истории.

Katz, History of Mathematics, 516–19, описывает геометрические аргументы Ньютона. Guicciardini, Reading the Principia, обсуждает, как современники Ньютона реагировали на «Начала» и в чем состояла их критика (некоторые их возражения звучали убедительно). Современный вывод законов Кеплера из закона обратных квадратов дается в книге: Simmons, Calculus Gems, 326–35.

Следует помнить, что Евклид был систематизатором и сообщал (без упоминания авторства) результаты других греческих математиков – Теэтета, Архита, Евдокса, Гиппократа и так далее. Неизвестно, какие результаты в «Началах» принадлежат самому Евклиду. Прим. пер .

Jones, John Couch Adams, и Sheehan and Thurber, John Couch Adams’s Asperger Syndrome.

Положение Нептуна рассчитали независимо друг от друга Адамс и Леверье. На самом деле Нептун оказался в 12° от положения, предсказанного Адамсом, и в 1° от положения, предсказанного Леверье. Для сравнения: видимый диаметр Луны составляет примерно 0,5°. Прим. пер .