Марио Ливио - φ – Число Бога. Золотое сечение – формула мироздания
- Название:φ – Число Бога. Золотое сечение – формула мироздания
- Автор:
- Жанр:
- Издательство:Литагент «АСТ»c9a05514-1ce6-11e2-86b3-b737ee03444a
- Год:2015
- Город:Москва
- ISBN:978-5-17-094497-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Марио Ливио - φ – Число Бога. Золотое сечение – формула мироздания краткое содержание
Как только не называли это загадочное число, которое математики обозначают буквой φ: и золотым сечением, и числом Бога, и божественной пропорцией. Оно играет важнейшую роль и в геометрии живой природы, и в творениях человека, его закладывают в основу произведений живописи, скульптуры и архитектуры, мало того – ему посвящают приключенческие романы! Но заслужена ли подобная слава? Что здесь правда, а что не совсем, какова история Золотого сечения в науке и культуре, и чем вызван такой интерес к простому геометрическому соотношению, решил выяснить известный американский астрофизик и популяризатор науки Марио Ливио. Увлекательное расследование привело к неожиданным результатам…
Увлекательный сюжет и нетривиальная развязка, убедительная логика и независимость суждений, малоизвестные факты из истории науки и неожиданные сопоставления – вот что делает эту научно-популярную книгу настоящим детективом и несомненным бестселлером.
φ – Число Бога. Золотое сечение – формула мироздания - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Приложение 1
Мы хотим доказать, что для любых целых чисел p и q, таких, что p > q, три числа: p 2 – q 2; 2 pq; p 2 + q 2формируют пифагорову тройку. Иначе говоря, нам надо доказать, что сумма квадратов первых двух чисел равна квадрату третьего.
Для этого мы обратимся к общим формулам сокращенного умножения, справедливым для любых a и b:
(a + b) 2 = (a + b) × (a + b) = a 2+ ab + ba + b 2 = a 2+ 2 ab + b 2
(a – b) 2 = (a – b) × (a – b) = a 2 – ab – ba + b 2 = a 2 – 2 ab – b 2.
На основании этих формул квадрат первого числа равен
(p 2 – q 2 ) 2 = p 4 – 2 p 2 q 2+ q 4.
Сумма первых двух квадратов равна
p 4 – 2 p 2 q 2+ q 4+ 4 p 2 q 2 = p 4+ 2 p 2 q 2+ q 4.
Квадрат третьего числа равен
(p 2+ q 2 ) 2 = p 4+ 2 p 2 q 2+ q 4.
Итак, мы видим, что квадрат третьего числа равен сумме квадратов первых двух чисел независимо от значений p и q.
Приложение 2
Мы хотим доказать, что диагональ и сторона правильного пятиугольника несоизмеримы, то есть у них нет общей меры.
Общий принцип доказательства по методу reductio ad absurdum приведен в конце главы 2.
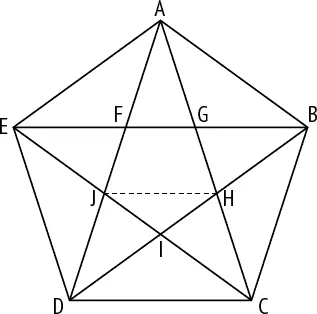
Обозначим сторону правильного пятиугольника ABCDE как s 1, а диагональ – как d 1. Из свойств равнобедренных треугольников легко вывести, что AB = AH и HC = HJ. Теперь обозначим сторону меньшего правильного пятиугольника FGHIJ как s 2и его диагональ как d 2. Очевидно, что
AC = AH + HC = AB + HJ.
Следовательно,
d 1 = s 1+ d 2или d 1 – s 1 = d 2.
Если у d 1и s 1есть какая-либо общая мера, значит, и d 1, и s 1представляют собой целое произведение этой общей меры. Следовательно, существует также общая мера d 1 – s 1, то есть d 2. Подобным же образом равенства
AG = HC = HJ
AH = AB
и
AH = AG + GH
AB = HJ + GH
дают нам
s 1 = d 2 + s 2
или
s 1 – d 2 = s 2.
Поскольку на основании нашего предположения общая мера для s 1и d 1представляет собой также общую меру для d 2, последнее равенство доказывает, что она же еще и общая мера для s 2. Поэтому мы обнаруживаем, что та единица, которая измеряет s 1и d 1, измеряет также s 2 and d 2. Продолжать этот процесс можно до бесконечности, рассматривая правильные пятиугольники все меньшего и меньшего размера. Тогда мы получим, что та же единица, которая служит общей мерой стороны и диагонали первого правильного пятиугольника, служит общей мерой и для всех других пятиугольников, сколь бы крошечными они ни становились. Поскольку очевидно, что так быть не может, следовательно, наше первоначальное предположение, что у стороны и диагонали правильного пятиугольника есть общая мера, ложно, что и доказывает, что s 1и d 1несоизмеримы.
Приложение 3
Площадь треугольника равна половине произведения его основания на высоту, проведенную к основанию. У треугольника TBC основание BC равно 2а , а высота ТА равна с . Следовательно, площадь треугольника равна с × а . Мы хотим показать, что если квадрат высоты пирамиды h 2равен площади ее треугольной стороны s × a, то s/a равно золотому сечению.
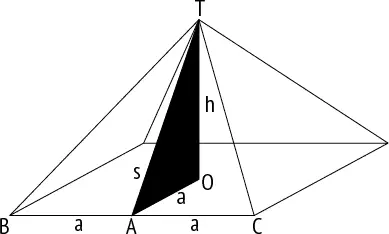
Дано, что
h 2 = s × a.
Применив теорему Пифагора к прямоугольному треугольнику TOA, получаем
s 2 = h 2 + a 2.
Теперь подставим значение h 2из первого равенства и получим
s 2 = s × a + a 2.
Разделим обе части на a 2и получим
(s/a) 2 = (s/a) + 1.
Иными словами, если мы обозначим s/a как x, у нас получится квадратное уравнение
x 2 = x + 1.
В главе 4 показано, что именно это уравнение и описывает золотое сечение.
Приложение 4
Одна из теорем в «Началах» доказывает, что если у двух треугольников одинаковые углы, эти треугольники подобны . А это значит, что форма у этих треугольников совершенно одинаковая и длины сторон соответственно пропорциональны. Если одна сторона одного треугольника вдвое длиннее соответствующей стороны второго треугольника, то это справедливо и по отношению к остальным сторонам.
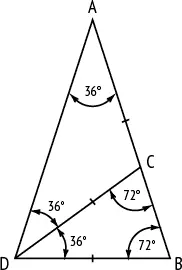
Треугольники ADB и DBC подобны, поскольку у них одинаковые углы. Следовательно, отношение AB/DB, то есть отношение сторон треугольников ADB и DBC, равно DB/BC, то есть отношению оснований этих треугольников.
AB/DB = DB/BC.
Однако эти треугольники также равнобедренные, поэтому
DB = DC = AC.
Из вышеприведенных равенств следует, что
AC/BC = AB/AC,
Что означает (согласно определению Евклида), что точка C делит отрезок AB в золотом сечении. Поскольку AD = AB и DB = AC, получаем также, что AD/DB = φ.
Приложение 5
Квадратные уравнения – это уравнения, имеющие вид
ax 2 + bx + c = 0,
где a, b, c – произвольные числа. Например, в уравнении 2 x 2+ 3 x + 1 = 0 имеем a = 2, b = 3, c = 1.
Общая формула для поиска двух корней уравнения:

В вышеприведенном примере
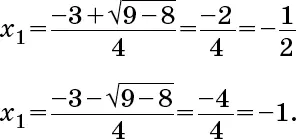
В уравнении, описывающем золотое сечение,
x 2 – x – 1 = 0,
a = 1, b = –1, c = –1, следовательно, корни:
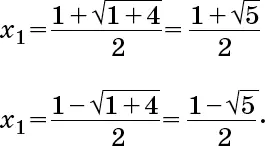
Приложение 6
Задачу о дележе наследства можно решить следующим образом. Обозначим все наследство как E, а долю каждого из сыновей в безантах – как x (по условию, все они делят наследство поровну).
Первый сын получил
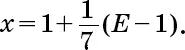
Второй сын получил
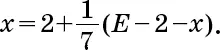
Приравниваем их доли:
Читать дальшеИнтервал:
Закладка:










