Марио Ливио - φ – Число Бога. Золотое сечение – формула мироздания
- Название:φ – Число Бога. Золотое сечение – формула мироздания
- Автор:
- Жанр:
- Издательство:Литагент «АСТ»c9a05514-1ce6-11e2-86b3-b737ee03444a
- Год:2015
- Город:Москва
- ISBN:978-5-17-094497-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Марио Ливио - φ – Число Бога. Золотое сечение – формула мироздания краткое содержание
Как только не называли это загадочное число, которое математики обозначают буквой φ: и золотым сечением, и числом Бога, и божественной пропорцией. Оно играет важнейшую роль и в геометрии живой природы, и в творениях человека, его закладывают в основу произведений живописи, скульптуры и архитектуры, мало того – ему посвящают приключенческие романы! Но заслужена ли подобная слава? Что здесь правда, а что не совсем, какова история Золотого сечения в науке и культуре, и чем вызван такой интерес к простому геометрическому соотношению, решил выяснить известный американский астрофизик и популяризатор науки Марио Ливио. Увлекательное расследование привело к неожиданным результатам…
Увлекательный сюжет и нетривиальная развязка, убедительная логика и независимость суждений, малоизвестные факты из истории науки и неожиданные сопоставления – вот что делает эту научно-популярную книгу настоящим детективом и несомненным бестселлером.
φ – Число Бога. Золотое сечение – формула мироздания - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
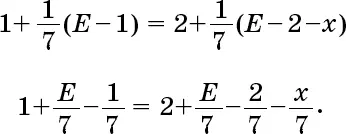
Упрощаем:
x/7 = 6/7
x = 6.
Следовательно, каждому из сыновей досталось по 6 безантов.
Подставив эту величину в первое равенство, получаем:
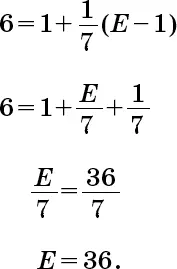
Сумма наследства составила 36 безантов. Следовательно, количество сыновей 36/6 = 6.
А вот как выглядит решение Фибоначчи.
Сумма наследства должна представлять собой такое число, чтобы если прибавить к нему 1 раз по 6, одно делилось бы на 1 плюс 6, то есть на 7, а если прибавить к нему 2 раза по 6, оно делилось бы на 2 плюс 6, то есть на 8, если же прибавить к нему 3 раза по 6, оно делилось бы на 3 плюс 6, то есть на 9, и т. д. Такое число – 36. 1/7 от (36 – 1/7) – это 35/7, плюс 1 – это 42/7, или 6, и это и есть сумма, которую получил каждый из сыновей; общая сумма наследства, поделенная на долю каждого из сыновей, дает нам число сыновей, то есть 36/6 равно 6.
Приложение 7
Отношение между количеством субобъектов n, коэффициентом сокращения длины f и числом измерений D равно
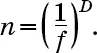
Если положительное число А записывается в виде А = 10 L , то L мы называем логарифмом (по основанию 10) числа А и записываем это так: L = log A. Иначе говоря, равенства А = 10 L и L = log A тождественны. Правила логарифмов таковы:
1. Логарифм произведения есть сумма логарифмов:
log (A × B ) = log A + log B.
2. Логарифм отношения есть разность логарифмов
log ( A / B ) =log A – log B.
3. Логарифм степени числа – это степень, умноженная на логарифм числа:
log A m = m × log A.
Поскольку 10 0 = 1, по определению логарифма log 1 = 0. Поскольку 10 1 = 10, 10 2 = 100 и так далее, получаем, что log 10 = 1, log 100 = 2 и т. д. Следовательно, логарифм любого числа от 1 до 10 – это число от 0 до 1, логарифм любого числа от 10 до 100 – это число от 1 до 2 и т. д.
Если мы возьмем логарифм (по основанию 10) обеих частей вышеприведенного равенства (описывающего отношения между n, f и D), то получим
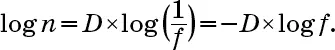
Если теперь поделить обе части на log f , мы получим
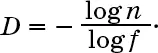
Скажем, в случае снежинки Коха каждая кривая содержит четыре «подкривые» в одну треть длины, поэтому n = 4, f = 1/3, и получаем
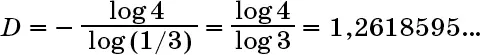
Приложение 8
Рассмотрим рис. 116, а , и увидим, что условие соприкосновения двух веток состоит в простом требовании, чтобы сумма всех горизонтальных длин постоянно уменьшающихся веток с длинами начиная от f 3была равна горизонтальной составляющей большой ветки длиной f. Все горизонтальные составляющие – это общая длина, умноженная на косинус угла, величиной 30 градусов. Поэтому получаем
f × cos 30° = f 3× cos 30° + f 4× cos 30° + f 5× cos 30° + …
Поделим это выражение на cos 30° – и получим
f = f 3 + f 4 + f 5 + f 6 + …
Сумма правой части – это сумма бесконечной геометрической прогрессии, то есть каждый ее член равен предыдущему, умноженному на константу, в которой первый член – это f 3, а отношение двух последовательных членов равно f. В целом сумма S бесконечной геометрической прогрессии с первым членом а и отношением последовательных членов q равна
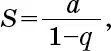
Например, сумма прогрессии
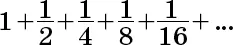
где a = 1 и q = 1/2, равна
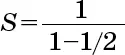
В нашем случае из вышеприведенного уравнения следует
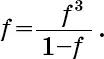
Делим обе части на f и получаем
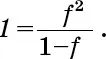
Умножаем на (1– f) , сокращаем и получаем квадратное уравнение
f 2 + f – 1 = 0,
положительный корень которого равен
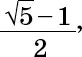
То есть 1/φ.
Приложение 9
Согласно закону Бенфорда, вероятность P, что цифра D появится на первом месте, составляет (логарифм по основанию 10)
P = log (1 + 1/D).
Следовательно, для D = 1
P = log (1 + 1) = log 2 = 0,30.
Для D = 2
P = log (1 + 1/2) = log 1,5 = 0,176,
И так далее. Для D = 9,
P = log (1 + 1/9) = log (10/9) = 0,046.
Согласно обобщенной формулировке закона вероятность того, что первые три цифры будут, к примеру, 1, 5 и 8, равна
P = log (1 + 1/158) = 0,0027.
Приложение 10
Доказательство Евклида, что существует бесконечное множество простых чисел, основано на методе reductio ad absurdum . Сначала Евклид предполагает, что верно противоположное: простых чисел существует лишь ограниченное множество. Однако, если это правда, одно из них должно быть самым большим простым числом. Обозначим самое большое простое число как P. Затем Евклид выводит новое простое число по следующему алгоритму: он перемножает все простые числа, начиная с 2 и до (включая) Р , и прибавляет к произведению единицу. Получается новое число
2 × 3 × 5 × 7 × 11 × … × P + 1.
Согласно первоначальному предположению, это должно быть не простое, а составное число, поскольку оно, очевидно, больше Р , а мы решили, что Р – самое большое простое число. Следовательно, это число должно делиться по крайней мере на одно из существующих простых чисел. Однако из его конструкции следует, что если мы разделим его на любое простое число вплоть до (и включая) Р , получится остаток 1. А следовательно, если бы это число и в самом деле составное, оно должно делиться на какое-то простое число больше Р . Однако это предположение противоречит первоначальному утверждению, что Р – самое большое простое число, и мы, таким образом, доказали, что простых чисел бесконечно много.
Читать дальшеИнтервал:
Закладка:










