Олег Власов - Футболоматика: как благодаря математике «Барселона» выигрывает, Роналду забивает, а букмекеры зарабатывают состояния
- Название:Футболоматика: как благодаря математике «Барселона» выигрывает, Роналду забивает, а букмекеры зарабатывают состояния
- Автор:
- Жанр:
- Издательство:Литагент 5 редакция
- Год:2018
- Город:Москва
- ISBN:978-5-04-091272-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Олег Власов - Футболоматика: как благодаря математике «Барселона» выигрывает, Роналду забивает, а букмекеры зарабатывают состояния краткое содержание
«Футболоматика» объясняет, как лучшие клубы мира конвертируют статистические данные в выигранные матчи. Вы убедитесь, что точные науки – один из краеугольных камней современного футбола.
Футболоматика: как благодаря математике «Барселона» выигрывает, Роналду забивает, а букмекеры зарабатывают состояния - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
12
Используемые здесь позиции адаптированы из книги Джонатана Уилсона «Переворачивая пирамиду: История футбольной тактики» (Orion Books, Лондон, 2008). Книга охватывает эти и многие другие формации, используемые в истории футбола.
13
Длина каждой из четырех ветвей, соединенных с пригородами, равна 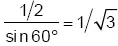 Применяя теорему Пифагора, средняя длина тогда
Применяя теорему Пифагора, средняя длина тогда 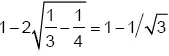 . Общая сумма равна
. Общая сумма равна 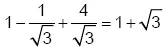 .
.
14
Tero, A. Rules for biologically inspired adaptive network design. – Science 327(5964), 2010. – p. 439–442.
15
Зоны, которые я вычисляю здесь, как я объясню ниже в основном тексте, представляют собой наборы точек, наиболее близкие к каждому игроку. Таким образом, все точки в игровых зонах – это те, которые ближе к этому игроку, и никакому другому. Это разбиение известно как диаграмма Вороного, в честь украинского математика Георгия Вороного.
16
Для вычисления триангуляции сначала используем диаграмму Вороного для расчета зон. Затем мы берем центральные точки всех зон диаграммы Вороного (то есть игроков) и рисуем связи между ними, если они имеют соседние зоны, чтобы создать триангуляцию Делоне. Для сети «Барселоны» первое и второе минимальное остовное дерево содержат большинство краев триангуляции Делоне. Триангуляции Делоне имеют тенденцию максимизировать углы в соединительных сетях, а диаграмма Вороного максимизирует размеры зон. Мы можем переключать взаимозаменяемость между двумя: каждая диаграмма Вороного имеет эквивалентную триангуляцию Делоне, и наоборот. Поэтому, когда мы максимизируем углы, мы максимизируем зоны, и наоборот.
17
Испанец равноудален от всех защитников, которые находятся поблизости ( прим. пер. ).
18
Для обзора см. Sumpter, D. J. The modelling cycle for collective animal behaviour. – Interface Focus 2(6), 2012. – p. 764–773.
19
Alvarez, G. A. & Franconeri, S. L. How many objects can you track? Evidence for a resource-limited attentive tracking mechanism. – Journal of Vision 7(13) – п. 14.1–14.10.
20
Michels, R. 2001. Teambuilding: The Road to Success – Reedswain Publishing, Spring City, PA, 2001. – p. 88
21
Техническая часть работы была выполнена Эмилем Розеном, студентом магистратуры моей исследовательской группы. Эмиль продолжил писать диссертацию, изучающую модели движения моей команды.
22
Moussaïd, M. Experimental study of the behav-ioural mechanisms underlying self-organization in humancrowds. – Proceedings of the Royal Society B: Biological Sciences. DoI: 10.1098/rspb.2009.0405.
23
Стрелки на рисунке 3.4 показывают только эффект неподвижного студента, а не общую тенденцию движущегося студента. В пустом коридоре движущийся студент идет вперед с относительно постоянной скоростью. Чтобы создать рисунок, это движение вперед в отсутствие неподвижного студента вычитается из движения, измеряемого в присутствии неподвижного студента, что и дает общий эффект.
24
В 148 испытаниях идущий студент прошел слева 60 раз (40,6 %) и справа 88 раз (59,4 %).
25
www.uefa.com/trainingground/skills/video/videoid=1654613.html
26
Pan, S. Pursuit, evasion and defense in the plane. – American Control Conference. IEEE, New York, 2012. – p. 4167–4173.
27
Stander, P. E. Cooperative hunting in lions: The role of the individual. – Behavioral Ecology and Sociobiology 29(6), 1992. – p. 445–454.
28
Ranganathan, S. Bayesian dynamical systems modelling in the social sciences. – PloS one 9(1), 2014. – e86468. Основной метод состоит в том, чтобы соответствовать направлению прохождения в качестве полиномиальной функции положения на поле. Как dx , так и dy компоненты направления передач устанавливаются в зависимости от положения х и y . Это дает хорошее представление о среднем направлении передач, хотя оно не позволяет зафиксировать изменение направления.
29
Взято из отчета 2007 года www.fifa.com/mm/document/fifafacts/bcoffsurv/emaga_9384_10704.pdf. FIFA признает, что это число является лишь приблизительной оценкой, и я даже не уверен, как это можно было бы надежно измерить. Но, учитывая всемирную популярность футбола, это звучит достаточно разумно.
30
Были некоторые исключения. Сезон-1986/87 завершился круговым турниром топ-команд, каждая из которых сыграла по 44 матча в чемпионате. В сезоне-1995/96 и 1996/97 в Ла Лиге было 22 команды.
31
Игра в угадайку не является очень надежной. Хороший пример ее неверности: я жив сегодня, был жив вчера и в течение примерно 15 тысяч дней. Следуя логике игры, вероятность того, что я завтра умру, составляет менее 1/15 000. Когда мне исполнится 100 лет, эта вероятность будет равна лишь 1/36 525. Чем дольше я живу, тем меньше шансов умереть! Все модели имеют свои ограничения, и моделист должен знать о них.
32
Официальная статистика Ла Лиги считает 40 голов Роналду. Эксперты Трофея Пичичи присудили один гол Пепе на счет Криштиану.
33
Представленная здесь форма – это распределение Гумбеля. Вероятность того, что топ-бомбардир забьет G или меньше голов, равна 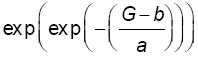 , где a = 5,44 и b = 26,9 являются параметрами, полученными из данных. Распределение Гумбеля является наиболее распространенной формой распределения экстремальных значений и наиболее подходящей, поскольку соответствует случаю, когда распределение выборок имеет экспоненциальный хвост.
, где a = 5,44 и b = 26,9 являются параметрами, полученными из данных. Распределение Гумбеля является наиболее распространенной формой распределения экстремальных значений и наиболее подходящей, поскольку соответствует случаю, когда распределение выборок имеет экспоненциальный хвост.
34
Здесь мы вычисляем вероятность того, что лучший бомбардир забил 50 или более голов в сезоне, а не вероятность того, что он забил ровно 50 голов.
35
В декабре 2017-го они сравнялись по полученным Золотым мячам ( прим. пер. ).
36
Sterl, A. An ensemble study of extreme storm surge related water levels in the North Sea in a chang-ing climate. – Ocean Science 5(3), 2009, – p. 369–378.
37
Эти и другие прогнозы сделаны в Van den Brink, H.W. & Können, G.P. Estimating 10 000-year return values from short time series. – International Journal of Climatology 31(1), 2011. – p. 115–126.
38
В оригинальном названии Bolt from the Blue акцент прежде всего сделан на фамилии Усэйна Болта ( прим. пер. ).
39
Усэйн завершил карьеру. Рекорд в 9,58 секунды пока не побит ( прим. пер. ).
40
Полный отчет МГЭИК можно найти на сайте ipcc-wg2.gov/SREX/report/.
41
Alexander, L.V. Global observed changes in daily climate extremes of temperature and precipitation. – Journal of Geophysical Research: Atmospheres 111(D5), 2006.
42
www.premierleague.com/en-gb/players/ea-sports-player-performance-index/what-is-the-ea-sports-ppi.html
43
McHale, I.G. On the development of a soccer player performance rating system for the English Premier League. – Interfaces 42(4), 2012. – p. 339–351.
44
Интервал:
Закладка:










