Олег Власов - Футболоматика: как благодаря математике «Барселона» выигрывает, Роналду забивает, а букмекеры зарабатывают состояния
- Название:Футболоматика: как благодаря математике «Барселона» выигрывает, Роналду забивает, а букмекеры зарабатывают состояния
- Автор:
- Жанр:
- Издательство:Литагент 5 редакция
- Год:2018
- Город:Москва
- ISBN:978-5-04-091272-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Олег Власов - Футболоматика: как благодаря математике «Барселона» выигрывает, Роналду забивает, а букмекеры зарабатывают состояния краткое содержание
«Футболоматика» объясняет, как лучшие клубы мира конвертируют статистические данные в выигранные матчи. Вы убедитесь, что точные науки – один из краеугольных камней современного футбола.
Футболоматика: как благодаря математике «Барселона» выигрывает, Роналду забивает, а букмекеры зарабатывают состояния - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
www.premierleague.com/en-gb/players/ea-sports-player-performance-index.html
45
В оригинале полное название звучит как “Moneyball: The art of winning an unfair game”.
46
Anderson, C. & Sally, D. The Numbers Game: Why everything you know about football is wrong. – Penguin, London, 2013.
47
www.optasportspro.com/about/optapro-blog/posts/2015/film-optapro-forum-beyond-shots/
48
www.theguardian.com/football/2015/jul/27/how- fc-midtjylland-analytical-route-champions-league-brentford-matthew-benham
49
Убедитесь сами: www.youtube.com/watch?v=yzvQCb-dAIZQ.
50
Златан почти 2 метра ростом, и когда он переворачивается с ног на голову, он разворачивается почти на 180°, поэтому начальная высота мяча при ударе также составляет около 2 метров. Начальная скорость мяча – v , угол – θ. Начальная скорость вверх равна v sinθ, а высота мяча за время t равна 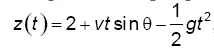 , где g = 9,8 м/с 2– ускорение свободного падения. Если не учитывать сопротивление воздуха, расстояние до ворот равно x ( t )= 27 vt cosθ, где 27 метров – это начальное расстояние до ворот.
, где g = 9,8 м/с 2– ускорение свободного падения. Если не учитывать сопротивление воздуха, расстояние до ворот равно x ( t )= 27 vt cosθ, где 27 метров – это начальное расстояние до ворот.
51
Мяч достигает цели, когда x(t) = 0. Это происходит в момент 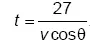 . Высота в этот момент равна
. Высота в этот момент равна 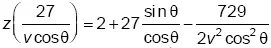 . Вопрос в том, для какой скорости v конечная высота будет равна от 0 до 2,44 (высота ворот)? Перестраивая это уравнение, получаем, что
. Вопрос в том, для какой скорости v конечная высота будет равна от 0 до 2,44 (высота ворот)? Перестраивая это уравнение, получаем, что 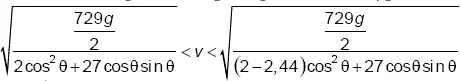 является условием забитого мяча. Это основа графиков на рисунке 5.3.
является условием забитого мяча. Это основа графиков на рисунке 5.3.
52
www.grc.nasa.gov/WWW/k-12/airplane/soccercode.html
53
Goff, J.E. Power and spin in the beautiful game. – Physics Today 63(7). – c. 62–63.
54
Hong, S. & Asai, T. Effect of panel shape of soccer ball on its flight characteristics. – Scientific Reports 4: 5068.
55
Гол, достойный мемориальной доски ( прим. пер. ).
56
Джеймс Хилл (1928–2015) – английский футболист; с 1973 по 1988 год был ведущим программы Match of the Day ( прим. пер. ).
57
Дэвид Нейри – шотландский футболист, игравший на позиции центрального защитника ( прим. пер. ).
58
Smallegange, I.M. & Van Der Meer, J. Interference from a game theoretical perspective: Shore crabs suffer most from equal competitors. – Behavioral Ecology 18(1), 2007. – с. 215–221; Smallegange, I.M. Assessment games in shore crab fights. – Journal of Experimental Marine Biology and Ecology 351(1), 2007. – p. 255–266.
59
Ричард Докинз – известный британский биолог, защитник геноцентричного взгляда на эволюцию ( прим. пер. ).
60
Nagy, M. Context-dependent hierarchies in pigeons. – Proceedings of the National Academy of Sciences 110(32), 2013. – p. 13049–13054.
61
Я провожу критерий суммы рангов с нулевой гипотезой, что нет разницы между количеством ничьих до и после изменения до трех очков. Значение р равно 0,0108.
62
Предположим, что если обе команды атакуют, тогда вероятность выигрыша вашей команды равна w , ничьей d , а поражения – l . Если одна из команд защищается, то вероятность победы или поражения умножается на p – эффективность защиты. Это дает следующие вероятности выигрыша, розыгрыша и проигрыша: pw, d + ( 1 – p ) w + ( 1 – p ) l, pl . В x -очковой системе слабая команда должна защищаться, если ( 1 – p ) w + ( 1 – p ) l > > xw ( 1 – p ), то есть l > ( x – 1 ) w . В системе двух очков за победу х = 2, то есть l > w . Слабая команда всегда должна обороняться. При х = 3 условие l > 2 w . Таким образом, слабая команда должна защищаться только в том случае, если вероятность поражения при атаке в два раза выше, чем при обороне.
63
Yasukawa, K. & Bick, E.I. Dominance hierarchies in dark-eyed juncos (Junco hyemalis): A test of a game-theory model. – Animal Behaviour, 31(2), 1983. – p. 439–448.
64
Kianercy, A. Critical transitions in a game theoretic model of tumour metabolism. – Interface Focus 4(4), 2014.
65
В оригинале используется Route One – речь о тактике игры в атаке, основанной на использовании длинного паса ( прим. пер. ).
66
Grund, T.U. Network structure and team performance: The case of English Premier League soccer teams. – Social Networks 34(4), 2012. – p. 682–690.
67
Когда команда владеет мячом, она пасует чаще чем 3–5 раз в минуту. Показатели занижены из-за того, что учитывают все время. Для полного определения скорости передач см. http://optasports.com/news-area/blog-optas-event-definitions.aspx.
68
http://espn.go.com/espnw/athletes-life/the-buzz/article/13173839/uswnt-teammates-unleash-their-abby-wambach-impressions
69
На этой карте больше соединительных линий, чем у Италии, Англии и Испании. Это из-за низкого порога: здесь я показываю пары от пяти успешных передач; для Евро этот показатель был равен 11 и больше.
70
Bearman, P.S. Chains of affection: The structure of adolescent romantic and sexual networks. – American Journal of Sociology 110(1), 2004. – p. 44–91.
71
Британская вариация произношения «тики-таки» ( прим. пер. ).
72
На момент написания книги Гвардиола действительно тренировал немецкий клуб – сейчас он занимает пост главного тренера в «Манчестер Сити» ( прим. пер .).
73
www.fourfourtwo.com/statszone/
74
Если говорить более конкретно, она представляет собой наименьшую форму, в которой мы можем провести прямую линию от любого из черных кругов до любого другого, не покидая самой фигуры.
75
«Разумно близкое» означает в пределах одного стандартного отклонения как в направлении влево/вправо, так и вверх/вниз.
76
Домашний стадион «Дерби» ( прим. пер. ).
77
Модель, которую я использую здесь, проистекает из эволюционной теории игр, впервые предложенной Джоном Мейнардом Смитом. Полагаю, что население лентяев имеет темпы роста, пропорциональные выгоде за уклонение минус средняя выгода населения. Это дает следующее уравнение: 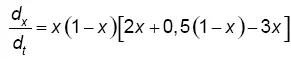 .
.
78
Предположим, вы читаете своей дочке 30 минут (у нее половина ваших генов). Значит, внуку вы читаете 30 × 2/32 = 1,875.
79
West, S.A. Sixteen common misconceptions about the evolution of cooperation in humans. – Evolution and Human Behavior 32(4), 2017. – p. 231–262.
80
Так команду «Селтик» стали называть после финала, который проходил в столице Португалии ( прим. пер. ).
81
Дэвид перепутал – в СССР золотые медали выдавали только за общие успехи в учебе; Валерий Васильевич окончил школу с серебряной медалью ( прим. пер. ).
82
Киевский политехнический институт ( прим. пер. ).
83
Интервал:
Закладка:










