Олег Власов - Футболоматика: как благодаря математике «Барселона» выигрывает, Роналду забивает, а букмекеры зарабатывают состояния
- Название:Футболоматика: как благодаря математике «Барселона» выигрывает, Роналду забивает, а букмекеры зарабатывают состояния
- Автор:
- Жанр:
- Издательство:Литагент 5 редакция
- Год:2018
- Город:Москва
- ISBN:978-5-04-091272-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Олег Власов - Футболоматика: как благодаря математике «Барселона» выигрывает, Роналду забивает, а букмекеры зарабатывают состояния краткое содержание
«Футболоматика» объясняет, как лучшие клубы мира конвертируют статистические данные в выигранные матчи. Вы убедитесь, что точные науки – один из краеугольных камней современного футбола.
Футболоматика: как благодаря математике «Барселона» выигрывает, Роналду забивает, а букмекеры зарабатывают состояния - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
128
К сожалению, после того как я написал это, подобная катастрофа снова повторилась при хадже в сентябре 2015 года. На этот раз погибло более 700 человек.
129
Среднее – сумма всех догадок, деленная на количество догадок, а медиана – это предположение посередине. Всего у меня 19 студентов. 9 из них предположили, что было менее 90 сладостей, и 9 из них предположили, что их было больше 90. Единственный студент, который предположил 90, является медианной догадкой.
130
Surowiecki, J. The Wisdom of Crowds. – Anchor, New York, 2005.
131
Книга Шуровьески начинается с описания эксперимента, проведенного Фрэнсисом Гальтоном на ярмарке, где среднее – 787 догадок о весе живого быка – было очень близко к правильному. Оригинальная работа Гальтона: Galton, F. Vox populi (the wisdom of crowds). – Nature 75(1949), 1907. – p. 450–451.
132
Максимальная догадка была установлена заранее на уровне 1500.
133
King, A. J. Is the true wisdom of the crowd to copy successful individuals? – Biology Letters 8(2), 2012. – с. 197–200.
134
В эксперименте Кинга ограничение не было установлено. Таким образом, один участник предположил 10 тысяч, еще двое считали, что конфет 5 тысяч. Это сделало среднее значение ненадежным, но никак не отразилось на медиане. Разница между средним и медианой поясняется в примечании 128.
135
Среднее равно
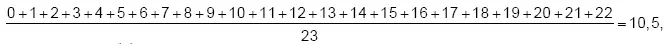
медиана – 11.
136
Berg, J. E. Prediction market accuracy in the long run. – International Journal of Forecasting 24(2), 2008. – p. 285–300.
137
Несмотря на прогнозы, консерваторы получили 37 % голосов, а лейбористы – 31 % ( прим. пер .).
138
http://prosoccertalk.nbcsports.com/2014/08/14/ pst-writers-predict-the-2014–15-premier-league-standings-do-you-agree/
139
Прочитать результаты и разбор Саймона вы можете в его блоге: https://scoreboardjournalism.wordpress.com.
140
Среднее равно
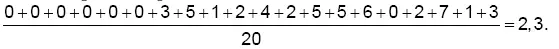
Обратите внимание, что здесь принимаются абсолютные разности: например, разность –4 принимается равной 4.
141
Я полагаю, что вышедшие в Премьер-лигу команды заняли 18-е, 19-е и 20-е места в зависимости от их позиции в Чемпионшипе сезоном ранее.
142
Речь об издании в Великобритании ( прим. пер .).
143
Из прогноза Принс-Райта сбылось немногое: «Ливерпуль» не попал ни в Лигу чемпионов, ни в Лигу Европы и «Норвич» вылетел ( прим. пер. ).
144
Проект совместно с голландским консультационным бюро Hypercube.
145
Ознакомиться с актуальным рейтингом вы можете на официальном сайте Euro Club Index https://www.euroclubindex.com/ ( прим. пер. ).
146
Для простоты мы предполагаем, что коэффициенты одинаковы для обеих команд.
147
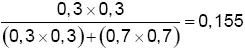 .
.
148
Sumpter, D.J.T. Collective Animal Behavior. – Princeton University Press, Princeton, NJ, 2010.
149
Ожидаемый результат для ничьей равен (0,25 × 3,4) + (0,75 × 0) = 0,85; для «Арсенала» (0,3375 × 3,1) + (0,6625 × 0) = 1,046.
150
Уравнение для того, сколько у меня осталось денег, выглядит так: 10 × 0,98 w , где w – количество недель.
151
Коэффициенты, которые я описываю здесь, были основаны на представленных на сайте www.oddsportal.com, где вы можете найти лучшие коэффициенты для каждого матча у ряда ведущих букмекеров. Затем я скорректировал коэффициенты, чтобы сделать их честными, то есть убрал из расчета выгоду букмекера.
152
1 / 1,33 = 75 % и 1 / 1,43 = 70 %.
153
Этот результат статистически значим. Вероятность того, что из 28 матчей 25 или более закончатся победой хозяев, равна 0,01 (при вероятности выигрыша в 72,5 %).
154
Этот метод описан более подробно в Jakobsson, R. & Karlsson, N. Testing market efficiency in a fixed odds betting market. – Working paper No. 12, Department of Statistics, Örebro University, 2007. Модель оптимальной логистической регрессии p (победа хозяев) 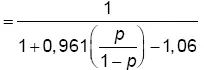 ,где p – букмекерская вероятность победы хозяев.
,где p – букмекерская вероятность победы хозяев.
155
http://papers.ssrn.com/sol3/papers.cfm?abstract_id= 1999459
156
В таблице ниже приведены три примера из первого тура сезона-2015/16.
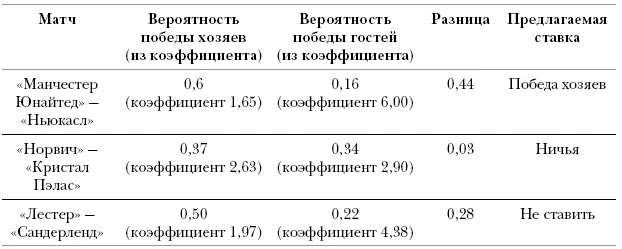
157
Grund, T. U. Network structure and team performance: The case of English Premier League soccer teams. – Social Networks 34(4), 2012. – p. 682–690.
158
На основе исследования, проведенного аналитической компанией Prozone. Подробнее см. www.theguardian.com/football/blog/2014/apr/27/bayern-munich-possession-football.
159
http://www.fourfourtwo.com/statszone
160
Мы уже обсуждали этот пункт в главе 7, и анализ, на котором он основывался, можно найти в статье Томаса Грунда (см. примечание 156).
161
Эти скорости занижены, поскольку включают в себя время, когда мяч находится вне игры: ауты, травмы и т. д. Однако они отражают относительную скорость передач команд и могут быть безопасно использованы при подгонке модели.
162
Рейтинги рассчитываются как 0,13 × (скорость передач) + + 0,76 log (ожидаемые забитые голы), что было показано логистической регрессией.
163
Мы устанавливаем коэффициенты следующим образом. Пусть вероятность букмекеров на победу одной команды равна p , а второй – q . Тогда, если | p – q | > 0,4, мы устанавливаем вероятность выигрыша стратегии как 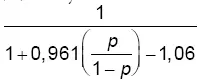 . Если | p – q | < 0,15, то вероятность ничьей равна 0,355 – 0,25 | p – q |. Все остальные вероятности результата берутся затем из коэффициентов букмекеров и корректируются соответствующим образом, чтобы отразить новую вероятность ничьей. При 0,15 ≤ | p – q | ≤ 0,4 ставка не делается.
. Если | p – q | < 0,15, то вероятность ничьей равна 0,355 – 0,25 | p – q |. Все остальные вероятности результата берутся затем из коэффициентов букмекеров и корректируются соответствующим образом, чтобы отразить новую вероятность ничьей. При 0,15 ≤ | p – q | ≤ 0,4 ставка не делается.
164
www.euroclubindex.com/asp/matchodds.asp.
165
Я продолжаю делать небольшую корректировку, потому что модель Пуассона слегка недооценивает ничьи. Остальные вероятности корректируются так, чтобы в сумме получать 1.
166
Я сделал модели и для забитых, и пропущенных голов и обнаружил следующие наилучшие модели с использованием регрессии Пуассона. Среднее количество голов за матч для домашней команды оценивается как exp (–0,7574 + 0,13 r + 0,76 h ), где r – скорость передач, h – среднее количество ожидаемых голов в предыдущих матчах. Среднее количество голов за матч для команды гостей оценивается как exp (–0,0784 + 0,5057 g + + 0,5527 b ), где g – среднее количество ожидаемых пропущенных хозяевами голов в предыдущих матчах. b = 1, если соперник команда гостей – «Челси», «Манчестер Сити», «Манчестер Юнайтед», «Арсенал», «Ливерпуль» или «Тоттенхэм»; b = 0 для всех остальных гостей.
Читать дальшеИнтервал:
Закладка:










