Николай Глинка - Общая химия

Так, согласно методу ВС, все ковалентные связи осуществляются общей парой электронов. Между тем, еще в конце прошлого века было установлено существование довольно прочного молекулярного иона водорода H 2 +: энергия разрыва связи составляет здесь 256 кДж/моль. Однако никакой электронной пары в этом случае образоваться не может, поскольку в состав иона H 2 +входит всего один электрон. Таким образом, метод ВС не дает удовлетворительного объяснения существованию иона H 2 +.

Далее, образование молекулы кислорода O 2, описывается методом ВС как результат создания двух общих электронных пар:

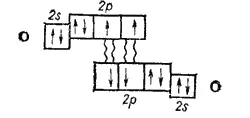
Согласно такому описанию, молекула O 2не содержит неспаренных электронов. Однако магнитные свойства кислорода указывают на то, что в молекуле O 2имеются два неспаренных электрона.

Каждый электрон, благодаря наличию у него спина, создает собственное магнитное поле. Направление этого поля определяется направлением спина, так что магнитные поля, образованные двумя спаренными электронами, взаимно компенсируют друг друга.

- 136 -

Поэтому молекулы, в состав которых входят только спаренные электроны, не создают собственного магнитного поля. Вещества, состоящие из таких молекул, являются диамагнитными — они выталкиваются из магнитного поля. Напротив, вещества, молекулы которых содержат неспаренные электроны, обладают собственным магнитным полем и являются парамагнитными; такие вещества втягиваются в магнитное поле.

Кислород — вещество парамагнитное, что свидетельствует о наличии в его молекуле неспаренных электронов.

На основе метода ВС трудно объяснить и то, что отрыв электронов от некоторых молекул приводит к упрочнению химической связи. Так, энергия разрыва связи в молекуле F 2составляет 155 кДж/моль, а в молекулярном ионе F 2 +- 320 кДж/моль; аналогичные величины для молекул O 2и молекулярного иона O 2 +составляют соответственно 494 и 642 кДж/моль.

Приведенные здесь и многие другие факты получают более удовлетворительное объяснение на основе метода молекулярных орбиталей (метод МО).

Мы уже знаем, что состояние электронов в атоме описывается квантовой механикой как совокупность атомных электронных орбиталей (атомных электронных облаков); каждая такая орбиталь характеризуется определенным набором атомных квантовых чисел. Метод МО исходит из предположения, что состояние электронов в молекуле также может быть описано как совокупность молекулярных электронных орбиталей (молекулярных электронных облаков), причем каждой молекулярной орбитали (МО) соответствует определенный набор молекулярных квантовых чисел. Как и в любой другой многоэлектронной системе, в молекуле сохраняет свою справедливость принцип Паули (см. § 32), так что на каждой МО может находиться не более двух электронов, которые должны обладать противоположно направленными спинами.

Молекулярное электронное облако может быть сосредоточено вблизи одного из атомных ядер, входящих в состав молекулы: такой электрон практически принадлежит одному атому и не принимает участия в образовании химических связей. В других случаях преобладающая часть электронного облака расположена в области пространства, близкой к двум атомным ядрам; это соответствует образованию двухцентровой химической связи. Однако в наиболее общем случае электронное облако принадлежит нескольким атомным ядрам и участвует в образовании многоцентровой химической связи. Таким образом, с точки зрения метода МО двухцентровая связь представляет собой лишь частный случай многоцентровой химической связи.

Основная проблема метода МО — нахождение волновых функций, описывающих состояние электронов на молекулярных орбиталях. В наиболее распространенном варианте этого метода, получившем сокращенное обозначение «метод МО ЛКАО» (молекулярные орбитали, линейная комбинация атомных орбиталей), эта задача решается следующим образом.

- 137 -

Пусть электронные орбитали взаимодействующих атомов характеризуются волновыми функциями ψ 1, ψ 2, ψ 3... и т. д. Тогда предполагается, что волновая функция ψ, отвечающая молекулярной орбитали, может быть представлена в виде суммы

ψ = C 1ψ 1+ C 2ψ 2+ C 3ψ 3+ ...

где C 1, C 2, C 3... - некоторые численные коэффициенты.

Для уяснения физического смысла такого подхода вспомним, что волновая функция ψ соответствует амплитуде волнового процесса, характеризующего состояние электрона (см. § 26). Как известно, при взаимодействии, например, звуковых или электромагнитных волн их амплитуды складываются. Как видно, приведенное уравнение равносильно предположению, что амплитуды молекулярной «электронной волны» (т. е. молекулярная волновая функция) тоже образуются сложением амплитуд взаимодействующих атомных «электронных волн» (т. е. сложением атомных волновых функций). При этом, однако, под влиянием силовых полей ядер и электронов соседних атомов волновая функция каждого атомного электрона изменяется по сравнению с исходной волновой функцией этого электрона в изолированном атоме. В методе МО ЛКАО эти изменения учитываются путем введения коэффициентов C 1, C 2и т. д., так что при нахождении молекулярной волновой функции складываются не исходные, а измененные амплитуды — C 1ψ 1, C 2ψ 2, и т. д.

Выясним, какой вид будет иметь молекулярная волновая функция ψ, образованная в результате взаимодействия волновых функций ( ψ 1и ψ 2) 1s-орбиталей двух одинаковых атомов. Для этого найдем сумму C 1ψ 1+ C 2ψ 2. В данном случае оба рассматриваемых атома одинаковы, так что коэффициенты C 1и C 2равны по величине (C 1=C 2=C), и задача сводится к определению суммы C(ψ 1+ψ 2). Поскольку постоянный коэффициент С не влияет на вид искомой молекулярной волновой функции, а только изменяет ее абсолютные значения, мы ограничимся нахождением суммы (ψ 1+ψ 2).

Для этого расположим ядра взаимодействующих атомов на том расстоянии друг от друга (r), на котором они находятся в молекуле, и изобразим волновые функции 1s-орбиталей этих атомов (рис. 43,а); каждая из этих функций имеет вид, показанный на рис. 9, а(стр. 76). Чтобы найти молекулярную волновую функцию ψ, сложим величины ψ 1и ψ 2: в результате получится кривая, изображенная на рис. 43,б. Как видно, в пространстве между ядрами значения молекулярной волновой функции ψ больше, чем значения исходных атомных волновых функций. Но квадрат волновой функции характеризует вероятность нахождения электрона в соответствующей области пространства, т. е. плотность электронного облака (см. § 26). Значит, возрастание ψ в сравнении с ψ 1и ψ 2означает, что при образовании МО плотность электронного облака в межъядерном пространстве увеличивается.