Ричард Фейнман - Том 1. Механика, излучение и теплота

Обратите внимание, что движение каждого из двух маятников — это колебания с циклически изменяющейся амплитудой. Поэтому движение одного из маятников можно, очевидно, рассматривать с различных точек зрения, в частности как сумму двух одновременных колебаний с мало отличающимися частотами. Таким образом должно быть возможно обнаружить в этой системе два других движения и утверждать, что поскольку система наша, безусловно, линейная, то мы видим суперпозицию этих двух решений. Действительно, легко найти два способа так запустить нашу систему, что каждый из них даст в результате идеальное абсолютно периодическое колебание с одной частотой. Движение, с которого мы начали, не строго периодично, оно не продолжается все время (один маятник постепенно передает свою энергию другому и изменяет свою амплитуду), но есть способы так начать движение, что не будет никаких подобных изменений. Как только вы узнаете, что это за способы, то сразу же поймете почему. Если, например, мы запустим оба маятника одновременно, то, поскольку длина их одинакова и пружинка в этом случае бездействует, оба маятника так и будут продолжать качаться все время вместе. (Разумеется, если нет трения и все достаточно хорошо подогнано.) С другой стороны, существует еще одна возможность создать строго периодическое движение, которое также имеет определенную частоту,— когда маятники, оттянутые вначале в разные стороны на точно равные расстояния, движутся в противоположных направлениях. Нетрудно сообразить, что пружинка немного увеличивает «восстанавливающую силу», возникающую из-за действия силы тяжести, и система колеблется с несколько большей частотой, чем в первом случае,— вот и все. Почему с большей? Да потому что пружинка тянет, помогая силе тяжести, и это делает систему более «жесткой», так что частота такого колебания чуть-чуть больше.

Итак, создать колебания с постоянной амплитудой в нашей системе можно двумя способами: либо оба маятника качаются все время вместе с одной частотой, либо они качаются в противоположных направлениях с несколько большей частотой.

Действительное же движение системы, поскольку она линейна, можно представить в виде суперпозиции этих двух способов. (Напомним, что предметом этой главы являются эффекты сложения двух движений с различными частотами.) Давайте подумаем, что произошло бы, если бы мы сложили эти два решения. Если в момент t=0 запустить оба эти движения (причем с равными амплитудами и одинаковой фазой), то сумма этих двух движений означает, что один маятник, на который каким-то образом воздействовало первое движение и противоположным образом воздействовало второе, должен оставаться на месте, тогда как другой маятник, двигаясь одинаково при обоих способах движения, качается с удвоенной амплитудой. С течением времени, однако, оба эти основных движения , существуя независимо одно от другого, медленно сдвигаются по фазе одно относительно другого. Это означает, что после достаточно большого промежутка времени, такого, что в первом движении произойдет, скажем, 900,5 колебания, а во втором — только 900, относительная фаза станет как раз обратной по отношению к тому, что было вначале. Иначе говоря, маятник, имевший вначале большую амплитуду, остановится, тогда как маятник, неподвижный вначале, начнет качаться изо всех сил!

Итак, мы видим, что такое сложное движение можно рассматривать в рамках идеи резонансов, когда энергия от одного маятника переходит к другому, или как суперпозицию двух движений с постоянной амплитудой и различными частотами.

В этой главе мы рассмотрим ряд замечательных явлений, возникающих в результате «заключения» волны в некоторую ограниченную область. Сначала нам придется установить несколько частных фактов, относящихся, например, к колебанию струны, а затем, обобщив эти факты, мы придем, по-видимому, к наиболее далеко идущему принципу математической физики.

Первый пример волн в ограниченном пространстве — это волны в пространстве, ограниченном с одной стороны. Давайте возьмем простой случай одномерной волны на струне. Можно было бы рассмотреть плоскую звуковую волну в пространстве, ограниченном с одной стороны стенкой, или какие-то другие примеры той же природы, но для наших теперешних целей вполне достаточно простой струны. Предположим, что один конец струны закреплен, ну, например, вмурован в «абсолютно жесткую» стенку. Математически это можно описать, указав, что перемещение струны у в точке x=0 должно быть нулем, ибо конец струны не может двигаться. Далее, если бы в этом деле не участвовала стенка, то, как мы знаем, общее решение, описывающее движение струны, можно было бы представить в виде суммы двух функций F ( x - ct ) и G ( x + ct ), причем первая описывает волну, бегущую по струне в одну сторону, а вторая — в другую, так что

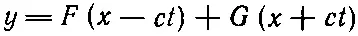(49.1)

будет общим решением для любой струны. Но нам, помимо этого, нужно еще удовлетворить условию неподвижности одного конца. Если в уравнении (49.1) мы положим х =0 и посмотрим, какие будут у в любой момент t , то получим y = F (- ct )+ G (+ ct ). Но эта сумма должна быть нулем в любой момент времени, а это означает, что функция G (+ ct ) должна быть равна - F (- ct ). Другими словами, функция G от некоторой величины должна быть равна функции - F от той же величины со знаком минус. Подставляя снова полученный результат в уравнение (49.1), находим решение поставленной задачи:

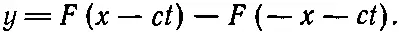(49.2)

Ясно, что это выражение всегда даст y=0, если х положить равным нулю.

На фиг. 49.1 представлена волна, идущая в отрицательном x-направлении вблизи точки х =0, и гипотетическая волна, идущая в противоположном направлении с обратным знаком и с другой стороны от начала координат.

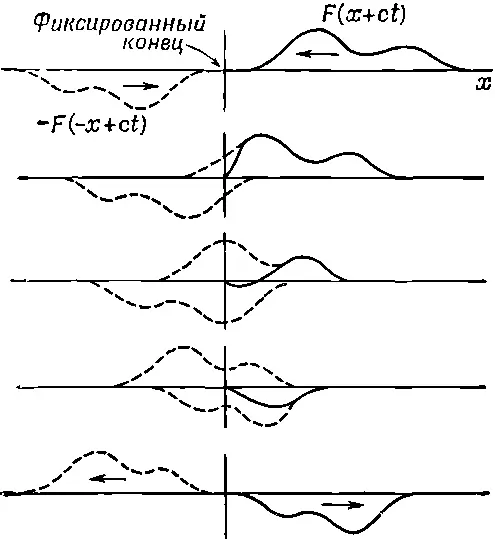
Фиг. 49.1. Отражение от стенки как суперпозиция двух бегущих волн.

Я сказал «гипотетическая», потому что с другой стороны, конечно, никакой колеблющейся струны нет. Истинное же движение струны должно рассматриваться как сумма этих двух волн в области положительных х . Достигнув начала координат, они в точке х =0 полностью уничтожат друг друга, а затем вторая (отраженная) волна, идущая, разумеется, в противоположном направлении, окажется единственной волной в области положительных х . Эти результаты эквивалентны следующему утверждению: волна, достигнув защемленного конца струны, отражается от него с изменением знака. Такое отражение всегда можно понять, если представить себе, как нечто дошедшее до конца струны вылетит затем из-за стены «вверх ногами». Короче говоря, если мы предположим, что струна бесконечна и что, где бы ни находилась волна, бегущая в одном направлении, всегда существует симметричная ей относительно точки х =0 другая волна, бегущая в противоположном направлении, то в самой точке х =0 никакого перемещения не будет, а поэтому безразлично, защемлена ли струна в этом месте или нет.