Ричард Фейнман - Том 1. Механика, излучение и теплота

Во всяком случае, телевизионная полоса начинается с частоты 54 Мгц . Первый телевизионный канал в Соединенных Штатах работает в полосе от 54 до 60 Мгц , т. е. имеет ширину 6 Мгц [37] В Советском Союзе изображение имеет 625 строк и ширина каналов несколько больше.— Прим ред. . «Постойте,— можете сказать вы,— ведь только сейчас мы доказали, что боковые полосы должны быть с обеих сторон, а поэтому ширина должна быть вдвое больше». Оказывается, радиоинженеры довольно хитрый народ. Если при анализе модулирующего сигнала использовать не только косинус, а косинус и синус, чтобы учесть разность фаз, то между высокочастотной и низкочастотной боковыми полосами обнаружится наличие определенного постоянного соотношения. Этим мы хотим сказать, что вторая боковая полоса не содержит никакой новой информации по сравнению с первой, так что одну из них вполне можно выкинуть. Приемник же устроен таким образом, что потерянная информация восстанавливается из несущей частоты и одной боковой полосы. Передача с помощью одной боковой полосы — очень интересный метод уменьшения ширины полосы, необходимой для передачи информации.

Следующий вопрос, который мы хотим обсудить,— это интерференция волн как в пространстве, так и во времени. Предположим, что в пространстве распространяются две волны. Вы, конечно, знаете, что распространение волны в пространстве, например звуковой, можно описать с помощью экспоненты exp[i(ωt- kx )]. Такая экспонента удовлетворяет волновому уравнению при условии, что ω 2=k 2с 2, где с — скорость распространения волны. В этом случае экспоненту можно записать в виде ехр[ik(x- ct )], что является частным случаем общего решения f ( x - ct ). Такая экспонента должна описывать волну, распространяющуюся со скоростью ω/k, равной с , и поэтому здесь все в порядке.

Давайте теперь складывать две такие волны. Пусть первая волна распространяется с одной частотой, а вторая волна — с какой-то другой. Случай неравных амплитуд рассмотрите самостоятельно, хотя существенного отличия здесь нет. Таким образом, мы хотим сложить exp[i(ω 1t-k 1x)]+exp[ i (ω 2 t - k 2 x )]. Это можно сделать с помощью математики, аналогичной использованной нами при сложении двух сигналов. Если скорости с обеих волн одинаковы, то сделать это очень легко; за исключением того, что вместо t стоит t '= t - х / с , это будет то же самое, что мы недавно проделали:

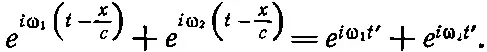(48.11)

При этом, естественно, мы получаем точно такие же модуляции, как и раньше, которые, однако, движутся вместе с волной. Другими словами, если сложить две волны, которые не просто осциллируют, но и перемещаются в пространстве, то получившаяся волна также будет двигаться с той же скоростью.

Хотелось бы обобщить это на случай волн, у которых отношение между частотой и волновым числом k не столь просто, например распространение волн в веществе с некоторым показателем преломления. В гл. 31 (вып. 3) мы уже изучали показатель преломления n и выяснили, что он связан с волновым числом следующим образом: k=nω/с. В качестве интересного примера мы нашли показатель преломления n для рентгеновских лучей:

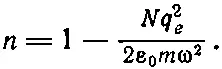(48.12)

На самом деле в гл. 31 мы получали и более сложные формулы, однако эта ничуть не хуже, так почему бы нам не взять ее в качестве примера.

Нам известно, что даже в том случае, когда ω и k не пропорциональны друг другу, отношение ω/k все равно будет скоростью распространения данной частоты и данного волнового числа. Это отношение называется фазовой скоростью , т. е. скоростью, с которой движется фаза или узел отдельной волны:

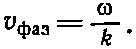(48.13)

Интересно, что, например, для случая распространения рентгеновских лучей в стекле эта фазовая скорость больше скорости света в пустоте [поскольку n, согласно (48.12), меньше единицы], а это несколько неприятно, ведь не думаем же мы, что можно посылать сигналы быстрее скорости света!

Обсудим теперь интерференцию двух волн, у которых значения ω и k связаны какой-то определенной зависимостью. Например, написанная ранее формула для показателя n говорит, что k есть определенная известная функция частоты ω. Для большей определенности давайте выпишем формулу зависимости k и ω в данной частной задаче:

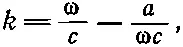(48.14)

где a = Nq e 2/2ε 0 m — постоянная. Во всяком случае, мы хотим сложить такие две волны, у которых для каждой частоты существует определенное волновое число.

Давайте сделаем это точно так же, как и при получении уравнения (48.7):

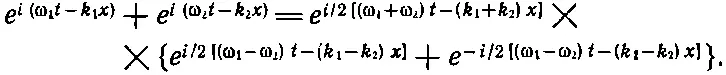(48.15)

Таким образом, снова получается модулированная волна, распространяющаяся со средней частотой и средним волновым числом, однако сила ее меняется в соответствии с выражением, зависящим от разности частот и разности волновых чисел.

Рассмотрим теперь случай, когда разности между двумя волнами относительно малы. Предположим, что мы складываем две волны с приблизительно равными частотами, при этом (ω 1+ω 2)/2 практически равно каждой из частот ω. То же можно сказать и о (k 1+k 2)/2. Таким образом, скорость волны, быстрых осцилляции, узлов действительно остается равной ω/k. Но смотрите, скорость распространения модуляций не та же самая! Как нужно изменить х , чтобы сбалансировать некоторую величину времени t? Скорость этих модулирующих волн равна

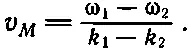(48.16)

Скорость движения модуляций иногда называют групповой скоростью . Если мы возьмем случай относительно малой разности между частотами и соответственно относительно малой разности между волновыми числами, то это выражение переходит в пределе в

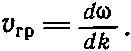(48.17)

Другими словами, чем медленнее модуляции, тем медленнее и биения, и вот что самое удивительное — существует определенная скорость их распространения, которая не равна фазовой скорости волны.