Ричард Фейнман - Том 1. Механика, излучение и теплота

Во-первых, рассмотрим скорость изменения кинетической энергии в общем трехмерном случае. Кинетическая энергия, когда движение имеет три измерения, равна

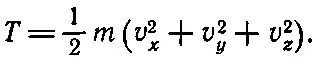
Дифференцируя ее по времени, получаем три устрашающих члена:

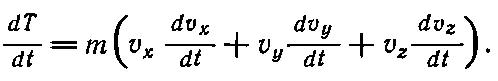(13.4)

Но ведь m ( dv x / dt ) — это сила F x , действующая на тело в направлении х . Значит, в правой части формулы (13.4) стоит F x v x + F y v y + F z v z . Призвав на помощь векторный анализ, вспоминаем, что это F· v.Итак,

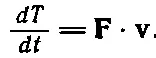(13.5)

А можно это вывести и быстрей: если аи b— два вектора, зависящих от времени, то производная от a· bравна

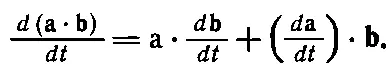(13.6)

Подставим сюда а=b=v:

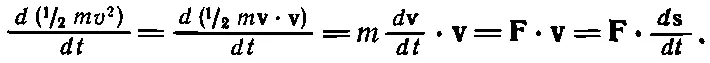(13.7)

Так как понятие кинетической энергии и вообще энергии очень важно, то различным величинам в этих уравнениях присвоены разные имена: 1/ 2 mv 2называется, как известно, кинетической энергией ; F· vназывается мощностью : сила, действующая на тело, умноженная («скалярно») на скорость тела, — это мощность, сообщаемая телу этой силой. Получается великолепная теорема: скорость изменения кинетической энергии тела равна мощности, затраченной силами, действующими на тело . Но для изучения сохранения энергии анализ следует продолжить. Давайте оценим изменение кинетической энергии за очень короткое время dt . Умножив обе части уравнения (13.7) на dt , найдем, что изменение кинетической энергии равно силе, скалярно умноженной на дифференциал пройденного расстояния

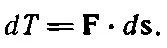(13.8)

А интегрируя, получаем

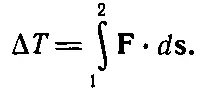(13.9)

Что это значит? Это значит, что, как бы и по какой бы кривой траектории ни двигалось тело под действием силы, все равно изменение в к. э. при переходе от одной точки кривой к другой равно интегралу от компоненты силы вдоль кривой, умноженной на дифференциал смещения ds (интегрирование от первой точки до второй). И у этого интеграла есть имя: его называют работой, совершенной силой над телом . Немедленно мы обнаруживаем, что мощность — это работа за секунду . И еще мы замечаем, что работу производит только составляющая силы вдоль направления движения . В нашем первом простом примере участвовали только вертикальные силы с одной-единственной составляющей F z, равной — mg . В этих обстоятельствах совершенно неважно, как тело движется, прямо вниз или по параболе, все равно от F·d s(которое можно написать как F x dx + F y dy + F z dz ) остается только F z dz =- mgdz , потому что прочие составляющие силы — нули. Значит, в этом случае

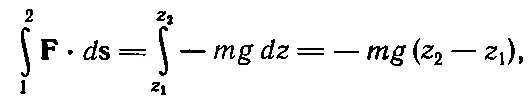(13.10)

так что в потенциальную энергию входит только высота, с которой тело падает.

Несколько слов о единицах. Так как сила измеряется в ньютонах, а для получения работы ее умножают на расстояние, то работу измеряют в единицах ньютон · метр , но большинство людей этого названия не любит, предпочитая название джоуль ( дж ). Это только другое слово, а единица та же. Итак, работу измеряют в джоулях. Мощность же — в джоулях в секунду; эту единицу называют ватт ( вт ). Если умножить ватты на время, то получим произведенную работу. Работу, которую местная энергосистема производит в наших квартирах (в техническом смысле), оценивается в ваттах, умноженных на время. Например, киловатт-час — это 1000 вт ×3600 сек , т. е. 3,6·10 6 дж .

Приведем еще несколько примеров работы и сохранения энергии. Рассмотрим тело, которое вначале имеет кинетическую энергию и быстро двигается, скользя по полу с трением. Оно останавливается. В начале кинетическая энергия не равна нулю, а в конце она равна нулю ; существует работа, произведенная силами, потому что раз есть трение, то есть и составляющая силы в направлении, противоположном направлению движения, и энергия постепенно теряется. Теперь рассмотрим массу на конце маятника, который качается в вертикальной плоскости в поле тяжести без трения. Здесь наблюдается нечто другое, потому что, когда масса опускается, сила направлена тоже вниз, а когда подымается, сила направлена в обратную сторону, так что у F·ds на спуске и на подъеме разные знаки. В соответствующих точках спуска и подъема значения F·ds равны по величине, но противоположны по знаку, так что в итоге интеграл есть чистый нуль. Поэтому кинетическая энергия в конце спуска в точности такая же, какой она была в начале подъема; это и есть принцип сохранения энергии. (Заметьте, что в присутствии сил трения сохранение энергии на первый взгляд не выполняется. Значит, нужно искать другую форму энергии. И действительно, оказывается, что когда два тела трутся друг о друга, то возникает тепло, мы же сейчас делаем вид, что об этом не знаем.)

Теперь займемся задачей потруднее, когда силы уже не постоянны и не направлены вниз, как раньше. Мы рассмотрим, например, движение планеты вокруг Солнца или спутника вокруг Земли.

Сперва мы рассмотрим движение тела, которое падает из точки 1 прямо на Солнце или на Землю (фиг. 13.2).

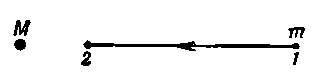
Фиг. 13.2. Падение малой массы m под действием тяжести на большую массу М.

Будет ли в этих обстоятельствах сохраняться энергия? Единственное отличие от того, что было раньше, — что теперь сила не постоянна, она меняется по мере падения. Мы знаем, что сила равна произведению GM / r 2на массу m падающего тела. Конечно, и теперь кинетическая энергия при падении возрастает, как возрастала и тогда, когда нас еще не волновало изменение силы с высотой. Вопрос только в том, можно ли отыскать иную, отличную от mgh , формулу для потенциальной энергии, найти другую функцию расстояния от Земли, чтобы для нее сохранение энергии не нарушалось.