Марк Волынский - Необыкновенная жизнь обыкновенной капли

Однако возникает вопрос: как же получилось, что не хватило уравнений и строгую логику пришлось заме­нить гипотезой? Победителей не судят, но если бы пред­положение ученого не оправдалось? Быть может, какой-то фактор выпал из рассмотрения, какие-то связи не были учтены? Вопрос законный, серьезный. Для ответа мобилизуем все ту же испытанную связку «опыт—тео­рия». Вглядимся внимательней в явление, вернувшись опять к форсунке. Но теперь приделаем к ней, продол­жая выходной канал, длинную прозрачную трубку — сопло из плексигласа. Раньше мы видели поток всегда с тыла или на выходе, сейчас можем взглянуть сбоку. Действительно, в профильной проекции обнаружилось нечто новое: у самого входа в сопло из камеры виднеет­ся крутая ступенька (иногда не одна) — резкое падение толщины жидкого колечка; внезапный рост радиуса вихря r m (рис. 10). Сразу появляется информация к размышлению: что за скачок? Где такое бывает? По­ищем аналогии — путь в науке очень полезный. Карто­тека памяти выдает необычный, запомнившийся образ: ведь это гидравлический прыжок, и возникает он дей­ствительно в потоках, сходных с нашим.

Гидравлики подробно изучают течение в открытом русле водослива (например, оросительный канал).

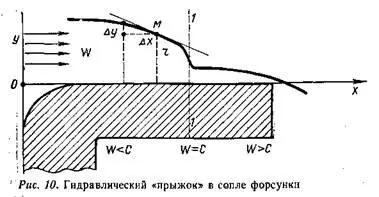
Жидкость там течет под действием силы тяжести — аналог потока с центробежным давлением в форсунке (оно тоже зависит от массы). Интересное это явление — гидравлический прыжок. Плавно ускоряясь, течет под уклон вода в канале по совершенно гладкому дну, уро­вень меняется медленно, равномерно. Но вот, разогнав­шись до какой-то предельной скорости, поток скачком меняет свою высоту, прыгает иногда почти отвесной стенкой, образуя один или несколько горбов-порогов. Потом на уменьшенном уклоне течение снова идет плав­но, но уже на другом уровне. Гидравлический прыжок возникает как раз в сечении, где скорость потока w до­стигает скорости с распространения поверхностных так называемых тяжелых волн *.

* Предположение о равенстве скорости течения жидкости в сопле форсунки скорости распространения тяжелых (центробежных) волн впервые было высказано И. И. Новиковым.

Из теории волнового дви­жения известна простая формула определения скорости распространения волн: c = √ gh, здесь g — ускорение под действием силы тяжести, h — высота уровня жид­кости.

Перенесем на форсунку это уравнение прыжка. Теперь система уравнений замыкается без каких-либо дополнительных гипотез, поскольку появилось новое со­отношение, определяющее радиус вихря, а именно ра­венство w и с:

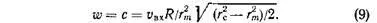
Вот оно, потерянное уравнение. Вместе со старыми уравнениями вся система приводит к принципу максимума расхода — теперь он уже не гипотеза, а следствие теории течения в форсунке.

В чем физический смысл условия w = c ? Скорость тяжелых волн с — это скорость передачи импульсов в разгоняющемся потоке. Они передают информацию сверху вниз по течению с помощью бегущей волны жидкости малой амплитуды: «Поток ускоряется, изда­ли меняйте форму течения, постепенно подстраивайте уровень жидкости на всем протяжении пути». Пока сиг­налы проходят по трассе, движение идет плавно, уро­вень меняется постепенно. Но вот жидкость к некоторо­му сечению разогналась до скорости волн — информа­ция уже не опережает потока жидкости, а движется параллельно с потоком, не оставляя времени для пере­стройки. Потому тесно, «задние напирают на перед­них», возникает так называемый кризис течения. И вот поток «взбунтовался», встает отвесной стеной, резким уступом, нарушив монотонность процесса. Произошел, естественно, и прыжок скорости, поскольку резко изме­нилось проходное сечение. Потом, на ином уровне подъ­ема, жидкость успокаивается, и снова течение стано­вится плавным. Значит, в крутящемся потоке нашей форсунки есть критическое сечение, где скорость равна критической, и это сечение в самом начале сопла. Даль­ше вниз по потоку, что ни делай, расход, формирующий­ся в истоке, уже не увеличишь, поток перед критическим сечением не перестроишь — туда просто не дойдут ника­кие импульсы-сигналы.

Итак, догадка Г. Н. Абрамовича о существовании максимума расхода подтвердилась экспериментом, экс­перимент помог найти аналогию между гидравлическим прыжком жидкости в открытом русле и режимом мак­симального расхода в форсунке с центробежным дав­лением.

Но, если мы взялись докапываться до самой сути, можно поставить новый вопрос: «А где же всеобщность исходных фундаментальных уравнений, о которых гово­рилось раньше? Они ведь должны предсказать все яв­ления, все опытные факты. Нельзя ли из самих исход­ных уравнений вывести гидравлический прыжок?»

Чтобы ответить на этот вопрос, вновь приходится возвратиться к истории этой проблемы, начиная с того периода, когда практика настойчиво потянула нашу связку «опыт—теория» на новый уровень.

Обычные виды топлива обладают заметной вяз­костью. Новые (для того времени) реактивные двигате­ли космических ракет и больших авиалайнеров, где чис­ло и разнообразие форсунок все возрастали, требовали более точных расчетов. Конструкция самой форсунки усложнялась, она обрастала различными клапанами, изготовлялась по все более высокому классу точности и становилась довольно дорогой деталью. Теория форсун­ки на основе идеальной жидкости сделала свое важное дело, но теперь уже не всегда давала нужную точ­ность.

Исследователи приняли эстафету дальнейшего дви­жения от теории идеальной жидкости к теории вязкой жидкости применительно к процессам в форсунке. Ин­женер Л. А. Клячко проводил испытания центробежной форсунки на топливах разной вязкости. Сначала в фор­сунку подавалось маловязкое топливо — бензин, затем более вязкое — керосин. Первые же опыты, к его удив­лению, показали парадоксальный результат: для керо­сина коэффициент расхода оказался больше, чем для бензина. Клячко сказал готовившему эксперимент ме­ханику:

— Быть этого не может: вязкость больше, а расход возрос. Что-то здесь не так! Вы, наверное, плохо уплот­нили форсунку, и керосин где-то подтекал.

— Форсунка собрана правильно, герметичность я га­рантирую,— с достоинством ответил опытный механик.

Повторный эксперимент (правильность сборки фор­сунки теперь проверяли вместе придирчивый инженер и задетый за живое механик) дал все тот же результат: на керосине коэффициент расхода больше, чем на бен­зине. Провели опыт с еще более вязким топливом — соляровым маслом. Коэффициент расхода опять возрос.