Марк Волынский - Необыкновенная жизнь обыкновенной капли

Первый закон — закон сохранения расхода: количе­ство жидкости, прошедшей через площадь f в секунду, то есть массовый расход, остается постоянным по всей трубке потока:

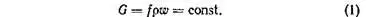
Уравнение (1) является гидродинамической формой закона сохранения вещества.

Частицы жидкости или газа ведут себя куда разум­нее людской толпы, они не замедляются, не толкутся в узких проходах, а, наоборот, если канал сужается ( f падает), жидкость протекает быстрее, при расшире­нии тракта ( f возрастает) скорость ее падает.

Второй закон — закон неизменности момента количе­ства движения: произведение скорости вращения и на радиус r сохраняется постоянным от одной струйки жидкости к другой. Применительно к форсунке это условие запишется так:

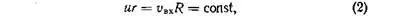
где v вх— скорость жидкости на входе в форсунку (на­чальная скорость закрутки), R — радиус камеры закру­чивания.

Вращающаяся жидкость — это «антикарусель»: чем меньше радиус вращения, тем больше скорость.

Третий закон — это закон сохранения энергии едини­цы объема жидкости (уравнение Бернулли): в уста­новившемся движении идеальной жидкости сумма по­тенциальной энергии единицы объема, то есть давления и кинетической энергии, обусловленной скоростью, со­храняется постоянной вдоль всей струйки тока, в нашем случае — от исходного давления Р 0 в резервуаре (балло­не) до выхода из канала. Уравнение Бернулли, связы­вающее параметры струйки, текущей сквозь форсунку, в различных поперечных сечениях имеет вид:

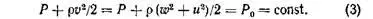
Здесь суммарная кинетическая энергия жидкости в сложном движении через сопло форсунки (где она идет по винтовым линиям) складывается из энергии по­ступательного движения со скоростью до и вращатель­ного — со скоростью и.

Удельная кинетическая энергия рv 2/2 по аналогии с первым слагаемым Р называется скоростным или дина­мическим напором Р g — эта энергия может перейти в давление. Если текущую жидкость остановить ладонью, то вы почувствуете суммарное давление Р+Р g, которое называется полным напором (с точностью до потерь на трение; эта сумма равна давлению в баллоне).

В медицине, например, используется полный напор струи для безыгольной инъекции вакцины. Специальный импульсный шприц подает кратковременную струю высокого давления. Это «жидкая игла» безболезненно про­калывает, точнее даже, пробивает кожу.

А вот новинка хирургии — «выстрел клеем»: специ­альный биологический клей вводят из пневмопистолета струей в зону операционного разреза. Механизм дей­ствия этого целебного пистолета таков. Клей, поданный под большим динамическим напором Р g в межклеточ­ное пространство живых тканей, сдавливает сосуды, останавливая кровотечение. Оставшийся на поверхности разреза клей образует корочку, способствующую зажив­лению. В обоих устройствах потенциальная энергия на­чального давления переходит сначала в кинетическую энергию, а потом, при ударе о поверхность, снова в дав­ление.

Из уравнения Бернулли видно, что давление и ско­рость — «антагонисты»: если вдоль потока v растет, то Р падает, и наоборот — с замедлением потока повыша­ется давление. На этом явлении основан, в частности, самый простой и экономичный распылитель — парик­махерский пульверизатор, дающий широкий факел с очень тонким распыливанием при малом расходе пар­фюмерии, что вполне устраивает и парикмахера, и кли­ента. Т-образная трубочка с перекладиной наверху опу­щена во флакон с жидкостью. Воздух из резиновой гру­ши под давлением поступает в трубку, где его скорость (согласно закону сохранения расхода) резко возра­стает: ведь трубочка намного уже, чем груша. Сле­довательно, давление, согласно уравнению Бернулли, упадет, и возникшее в перекладине разрежение по вертикальной трубочке будет засасывать жидкость вверх. Там быстрый поток воздуха погонит ее к вы­ходу на другом конце перекладины, распыливая на ка­пельки.

Уравнение Бернулли позволяет просто получить при­ближенные формулы для скорости истечения и расхода жидкости из отверстия распылителя в атмосферу. За­пишем уравнение сохранения энергии (3) между на­чальным сечением в баллоне, где давление равно Р о, а скорость течения жидкости почти нулевая (баллон очень широк сравнительно с отверстием), и сечением выхода в атмосферу с давлением Р а :

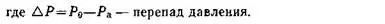
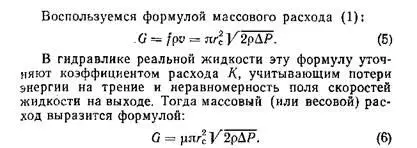
Для форсуночных и капельных нужд нам хватило трех уравнений сохранения, но мы упоминали еще о четвертом. Оно знаменательно, в частности, тем, что приводит к формуле для реактивной тяги двигателя, ле­жащей в основе всей ракетной техники. Вспомним про­стой и общеизвестный пример. Вы стоите в неподвиж­ной лодке на озере и бросаете тяжелый камень с кор­мы — лодка двинулась в противоположную сторону. Объяснение дает закон сохранения количества движе­ния (или импульса), из которого вытекает важное след­ствие: положение центра тяжести (или центра масс) системы под действием внутренних сил остается неиз­менным. До броска центр тяжести лодки со всем содер­жимым покоился в некоторой точке. Когда мы выброси» ли камень, часть массы системы ушла назад, распреде­ление масс изменилось, но центр тяжести «не имеет права» перемещаться. Чтобы сохранилось его прежнее положение в пространстве, лодка должна ‘была двинуть­ся вперед. То же и с ракетой: до запуска она была не­подвижной, но когда массы газа стали вытекать из со­пел, ракета, подчиняясь общему закону, полетела в противоположную сторону. Мощные струи газа будут вытекать из ракеты, сама она унесется далеко в космос, а центр тяжести системы «газы—ракета» останется по- прежнему в своей исходной точке, на земле. Закон ко­личества движения гласит: импульс сил — произведение сил на время их действия — равен изменению количе­ства движения всех тел в системе.

Если этот закон применить к ракете, получим фор­мулу тяги:

P = Gw c (7)