Ричард Фейнман - 3. Излучение. Волны. Кванты

§ 5. Математическое описание интерференции

Мы рассматривали излучение диполей с качественной точки зрения, теперь рассмотрим количественную картину. Найдем прежде всего суммарное поле от двух источников в самом общем случае, когда разность фаз а и силы осцилляторов a 1 и А 2 произвольны; для этого необходимо сложить два косинуса с одинаковой частотой, но разными фазами. Разность фаз находится весьма просто: она складывается из разности, возникаю­щей за счет неодинакового удаления точки наблюдения от обоих источников, и внутренней, заданной разности фаз колебаний. Выражаясь математически, нам необходимо сложить две волны: R=a[cos(wt+j 1 )+А 2 cos (wt+j 2 ). Как это сделать?

Каждый, вероятно, сумеет провести это сложение, но тем не менее проследим за ходом вычислений. Прежде всего, если мы разбираемся в математике и достаточно ловко управляемся с синусами и косинусами, эту задачу легко решить. Самый про­стой случай, когда амплитуда a 1равна А 2, и пусть обе они обозначаются через А. В этих условиях (назовем это тригоно­метрическим методом решения задачи) мы имеем

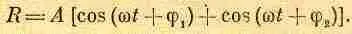(29.9)

На уроках тригонометрии вы, вероятно, доказывали равенство

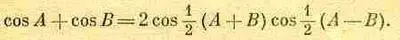(29.10)

Если это нам известно, то мы немедленно получаем R:

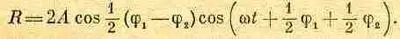(29.11)

Итак, мы снова получили синусоидальную волну, но с новой фазой и новой амплитудой. Вообще результат сложения двух синусоидальных волн есть синусоидальная волна с новой ам­плитудой A R , называемой результирующей амплитудой, и но­вой фазой j R, называемой результирующей фазой. В нашем частном случае результирующая амплитуда равна

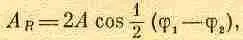(29.12)

а результирующая фаза есть арифметическое среднее обеих фаз. Таким образом, поставленная задача полностью решена. Предположим теперь, что мы забыли формулу сложения ко­синусов. Тогда можно применить другой метод решения — гео­метрический. Косинус, зависящий от wt, можно представить в виде горизонтальной проекции некоторого вращающегося век­тора. Пусть имеется вектор А 1, вращающийся с течением вре­мени; длина его равна a 1 , a угол с осью абсцисс равен wt+j 1. (Мы пока опустим слагаемое w t; как мы увидим, при выводе это не играет роли.) Сделаем моментальный снимок векторов в момент времени t =0, помня, что на самом деле вся схема вращается с угловой скоростью w (фиг. 29.9). Проекция a1 на ось абсцисс в точности равна a1cos (wt+j 1). В момент времени t = 0 вторая волна представляется вектором А 2, длина которого равна a2 , а его угол с осью абсцисс равен j 2, причем он тоже вращается с течением времени.

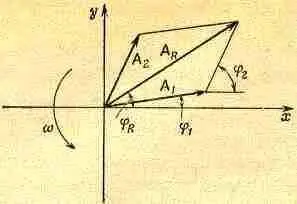
Фиг. 29.9. Геометрический способ сложения двух косинусоидаль­ных волн.

Чертеж вращается со скоростью w против часовой стрелки.

Оба вектора вращаются с одинаковой угловой скоростью w, и их относительное распо­ложение неизменно. Вся система вращается жестко, подобно твердому телу.

Горизонтальная проекция А 2равна A 2 cos( w t + j 2). Из векторного анализа известно, что при сложении двух векторов по правилу параллелограмма образуется новый, ре­зультирующий вектор А R, причем

x-компонента его есть сумма х-компонент слагающих векторов. Отсюда получаем решение нашей задачи. Легко проверить, что получается правильный ответ в нашем частном случае a 1 =А 2 =А. Действительно, из фиг. 29.9 очевидно, что A R лежит посредине между a 1и А 2и составляет угол 1/2 (j 2-j 1) с каждым из них. Следовательно, A R = 2А cos 1/ 2(j 2-j 1), что совпадает с прежним результатом. Кроме того, в случае А 1- А 2фаза A Rесть среднее от фаз a 1и А 2. Для неравных A 1и А 2 задача решается столь же просто. Мы можем назвать это геометрическим решением задачи.

Существует еще один метод решения задачи, его можно было бы назвать аналитическим. Вместо того чтобы рисовать схему, подобную приведенной на фиг. 29.9, напишем выраже­ния, имеющие тот же смысл, что и чертеж, и сопоставим каж­дому вектору комплексное число. Действительные части этих комплексных чисел отвечают реальным физическим величинам. В нашем конкретном случае волны записываются следующим образом: A 1ехр[i(wt+j 1)] [действительная часть этого равна A 1cos(wt+j 1)] и A 2ехр[i(wt-+j 2)]. Сложим обе волны:

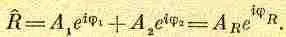(29.13)

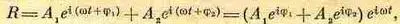(29.14)

Задача, таким образом, решена, так как мы имеем окончатель­ный результат в виде комплексного числа с модулем A Rи фа­зой j R.

Для иллюстрации аналитического метода найдем амплитуду А R , т. е. «длину» R. «Длина» комплексного числа в квадрате есть само комплексное число, умноженное на сопряженное ему.

Комплексное сопряжение состоит в изменении знака i . Отсюда получаем

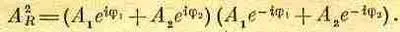(29.15)

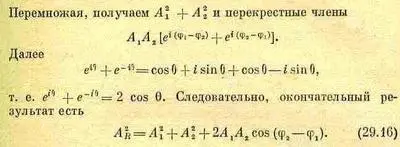
(С помощью формул тригонометрии легко установить совпаде­ние получаемого результата с длиной A Rна фиг. 29.9.)

Итак, суммарная интенсивность складывается из члена А 1 2, возникающего от действия только первого источника, интенсив­ности А 2 2 , равной интенсивности второго источника, и еще дополнительного члена. Этот дополнительный член мы назовем эффектом интерференции. Он представляет собой разность между истинным результатом сложения и суммой интенсивностей. Интерференционный член может быть как положительным, так и отрицательным. [Интерференция (interference) в англий­ской разговорной речи означает возражение, помеху, но в фи­зике слова часто теряют первоначальный смысл и употребляются совсем в другом значении!] Если интерференционный член по­ложителен, мы будем говорить о конструктивной интерферен­ции (буквальный смысл этого выражения покажется ужасным всем, кроме физиков!). В противном случае мы говорим о дест­руктивной интерференции.