Е. Неискашова - Алгебра. 9 класс. 50 типовых вариантов экзаменационных работ для подготовки к ГИА
- Название:Алгебра. 9 класс. 50 типовых вариантов экзаменационных работ для подготовки к ГИА
- Автор:
- Жанр:
- Издательство:Array Литагент «Аудиокнига»
- Год:2009
- Город:Москва
- ISBN:978-5-17-059843-4,978-5-271-24146-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Е. Неискашова - Алгебра. 9 класс. 50 типовых вариантов экзаменационных работ для подготовки к ГИА краткое содержание
Каждый вариант составлен в полном соответствии с требованиями государственной итоговой аттестации и включает задания разных типов и уровня сложности по всем основным темам, которые выносятся на экзамен: числа, буквенные выражения, преобразования алгебраических выражений, уравнения, неравенства, последовательности и прогрессии, функции и графики.
Значительный по объему банк экзаменационных материалов предоставляет отличную возможность для интенсивной тренировки и овладения необходимыми для успешной сдачи экзамена умениями и навыками.
В конце книги даны ответы для самопроверки на все задания.
Алгебра. 9 класс. 50 типовых вариантов экзаменационных работ для подготовки к ГИА - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
При выполнении заданий 17–21 используйте отдельный подписанный лист. Сначала укажите номер задания, а затем запишите его решение .
17. Постройте график функции у = 1/ 2 x 2+ x + 2. Укажите наименьшее значение этой функции.
18. Решите неравенство
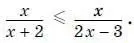
19. Найдите значение k и второй корень уравнения x 2+ kx + 8 = 0, если известно, что один из корней уравнения равен −4.
20. Два комбайна разной мощности, работая вместе, убирают с участка кукурузу за 8 часов. Если бы первый комбайн работал один в течение 4,5 часов, а затем второй работал бы один в течение 3 часов, то они убрали бы 50 % всей кукурузы. За сколько часов первый комбайн, работая один, может убрать кукурузу со всего участка?
21. Найдите все значения параметра k , при каждом из которых уравнение
| x − 2 | = kx + 1
имеет единственное решение.
Вариант 4
1. Расположите в порядке возрастания числа 0,0206; 0,02; 0,602.
1) 0,0206; 0,602; 0,02;
2) 0,0206; 0,02; 0,602
3) 0,02; 0,0206; 0,602
4) 0,602; 0,0206; 0,02.

3. Дневная норма потребления витамина С составляет 60 мг. Один апельсин в среднем содержит 45 мг витамина С . Сколько (приблизительно) процентов дневной нормы витамина С получил человек, съевший один апельсин?
1) 75 %; 2) 133 %; 3) 13,3 %; 4) 7,5 %.
4. Найдите значение выражения a ( b + c ), если a = 8,4, b = −1,2, c = 3,7.
1) 21;
2) 41,16;
3) −21;
4) 0,21.
5. Один килограмм творога стоит а рублей. Составьте выражение для вычисления стоимости (в руб.) b грамм этого творога.

6. В каком случае выражение преобразовано в тождественно равное?
1) 5( у − x ) = 5 у − x ;
2) (5 − x )( x + 5) = x 2− 25;
3) (5 − у ) 2= 25 − у 2;
4) (5 + у ) 2= 25 + 10 у + у 2.
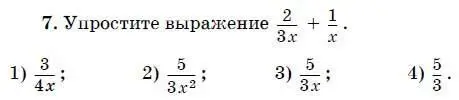
8. Найдите частное
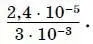
Ответ запишите в виде десятичной дроби.
Ответ: ____
9. Решите уравнение 4 − 2 х = 6 − 3( х + 2).
Ответ:____
10. Прямая у = 2 х пересекает параболу у = х 2+ х − 2 в двух точках. Вычислите координаты точки А .
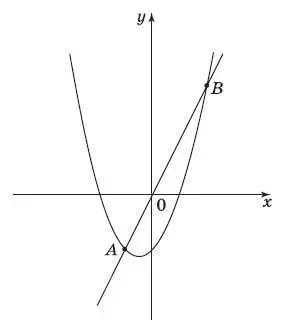
Ответ:____
11. Прочитайте задачу: «Пешеход рассчитал, что, двигаясь с определенной скоростью, расстояние от поселка до станции он пройдет за 1,2 часа. Но, увеличив свою скорость на 1 км/ч, он прошел это расстояние за 1 час. Найдите расстояние от поселка до станции.»
Выберите уравнение, соответствующее условию задачи, если буквой x обозначено расстояние (в км) от поселка до станции.

12. Решите неравенство 10 x − 3(3 x − 2) < 4.
1) x < −2;
2) x < 10;
3) x < 6;
4) x < 2.
13. На рисунке изображен график функции у = x 2+ 5 x . Используя график, решите неравенство x 2+ 5 x > 0.
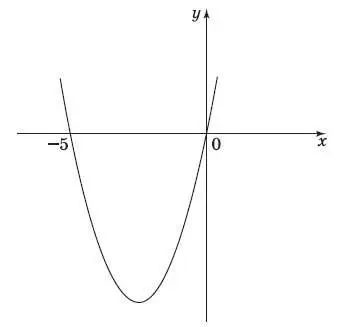
1) (− ∞; 0);
2) (− ∞; −5)U(0; + ∞);
3) (−5; 0);
4) (−5; + ∞).
14. Для каждой арифметической прогрессии, заданной формулой n -го члена, укажите ее разность d . (В таблице под каждой буквой запишите номер ответа, под которым указана соответствующая разность.)
A) a n = 3 n + 2; Б) b n = 5 n + 3; В) c n = 2 n − 5.
1) d = −5; 2) d = 3; 3) d = 2; 4) d = 5.

15. График какой квадратичной функции изображен на рисунке?
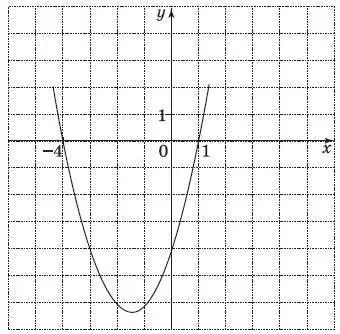
1) у = x 2+ 3 х − 4;
2) у = х 2− 3 х − 4;
3) у = − х 2− 5 х − 4;
4) у = − х 2+ 5 х − 4.
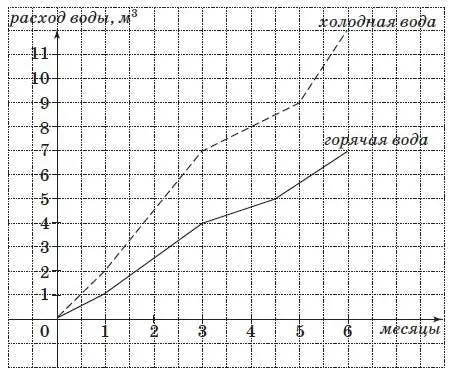
16. На рисунке изображен график движения пешеходов: первого – из пункта А в пункт В, второго – из пункта В в пункт А . (По горизонтальной оси откладывается время, прошедшее с момента начала движения – в минутах, а по вертикальной – расстояние, пройденное за это время – в км.) На каком расстоянии от пункта В произошла встреча этих пешеходов? С какой скоростью (в км/ч) шел каждый из этих пешеходов?
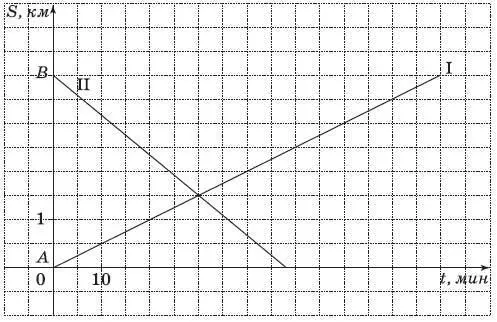
Ответ:___
При выполнении заданий 17–21 используйте отдельный подписанный лист. Сначала укажите номер задания, а затем запишите его решение.
17. Постройте график функции
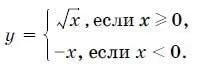
Укажите наименьшее значение этой функции.
18. Решите неравенство
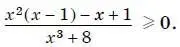
19. Упростите выражение
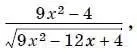
если известно, что x < 0,5.
20. Один рабочий взялся выполнить некоторый заказ за 10 дней при условии, что в течение 3 дней ему будет помогать второй рабочий. Если бы этот заказ было поручено выполнить каждому рабочему в отдельности, то на его выполнение первому рабочему потребовалось бы на 6 дней больше, чем второму. За сколько дней может выполнить этот заказ второй рабочий, работая один?
21. Найдите все значения параметра k, при каждом из которых прямая у = kx пересекает в трех различных точках ломаную, заданную условиями
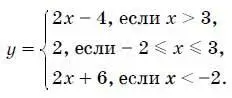
Вариант 5

2. Какое из чисел√ 3; √1800; √3600 является рациональным?
Читать дальшеИнтервал:
Закладка:










