Е. Неискашова - Алгебра. 9 класс. 50 типовых вариантов экзаменационных работ для подготовки к ГИА

Ответ :______

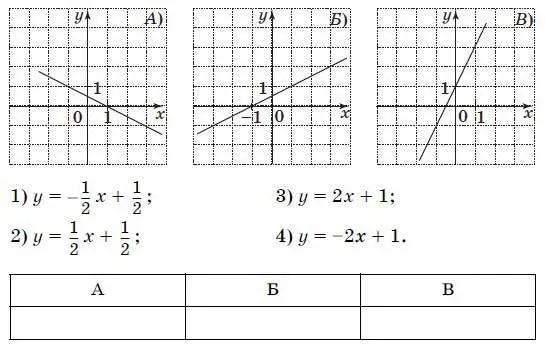
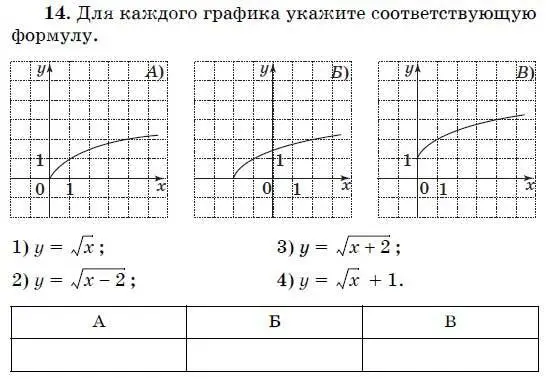
15. Для каждого графика укажите соответствующую формулу.

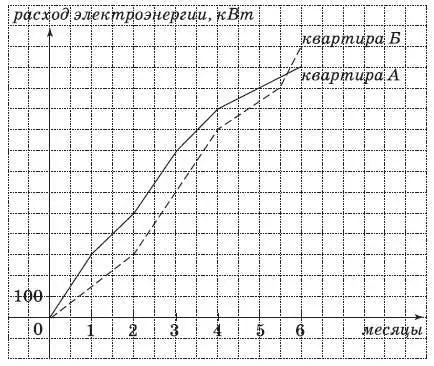
16. На рисунке представлены показания приборов учета потребления электроэнергии в двух квартирах А и Б в течение первого полугодия. (По горизонтальной оси откладывается время, прошедшее с начала года – в месяцах, а по вертикальной – количество электроэнергии, израсходованной за это время – в кВт.) Определите, в какой из квартир расход электроэнергии во втором квартале (4, 5, 6 месяцы) был больше, и на сколько?

Ответ:______

При выполнении заданий 17–21 используйте отдельный подписанный лист. Сначала укажите номер задания, а затем запишите его решение.

17. Упростите выражение

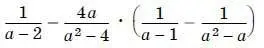
при а ≠ ±2, а ≠ 1, а ≠ 0.

18. Найдите область определения функции

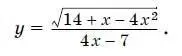
19. Решите систему уравнений

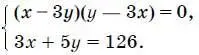
20. Из города А в город В выехал велосипедист. Спустя 48 мин вслед за ним выехал мотоциклист, скорость которого на 30 км/ч больше скорости велосипедиста. Через 36 мин после своего выхода мотоциклист, обогнав велосипедиста, оказался на расстоянии 6 км от него. Найдите скорость велосипедиста, зная, что велосипедист и мотоциклист двигались с постоянными скоростями и без остановок.

21. Найдите все значения параметра а, при каждом из которых график функции у = x 2+ 2 a | x | − a 2пересекает прямую у = a − 6 в четырех различных точках.

1. Численность населения Италии составляет 6 × 10 7человек, а Венгрии – 9,9 × 10 6человек. Во сколько раз численность населения Италии больше численности населения Венгрии?

1) примерно в 6 раз;

2) примерно в 16,5 раз;

3) примерно в 0,6 раза;

4) примерно в 60 раз.

2. Некоторый товар поступил в продажу по цене 800 руб. В течение первой недели продаж его цена оставалась неизменной. В начале второй недели цена товара была снижена на 10 %, а в начале третьей недели цена товара была снижена еще на 15 %. По какой цене продавался товар в течение третьей недели?

1) 600 руб.;

2) 200 руб.;

3) 612 руб.;

4) 188 руб.

3. Расположите числа 7; 4√3; 8 в порядке возрастания.

1) 4; 4√3; 8;

2) 4√3; 7; 8;

3) 8; 7; 4√3;

4) 8; 4√3; 7.

4. Даны выражения

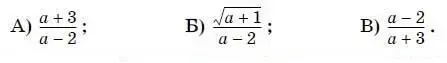
Какие из этих выражений не имеют смысла при a = 2?

1) Только А;

2) только Б;

3) только В;

4) А и Б.

5. Зная скорость и время движения, можно найти пройденное расстояние s по формуле s = vt , где v – скорость движения, t – время движения. Какое расстояние прошел человек за 12 мин, если известно, что скорость его движения равна 3 км/ч? Ответ выразите в километрах.

Ответ:____

6. Укажите выражение, тождественно равное произведению (5 − 4 x )(7 x − 2).

1) (4 x − 5)(7 x − 2);

2) −(4 x − 5)(7 x − 2);

3) (5 − 4 x )(2 − 7 x );

4) −(4 x − 5)(2 − 7 x ).

7. Найдите значение выражения

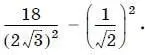
Ответ:____

8. В какой многочлен можно преобразовать выражение

2(4 − 3 a ) − ( a − 3) 2?

1) − a 2− 1;

2) − a 2− 12 a − 1;

3) − a 2− 12 a + 17;

4) − a 2+ 17.

9. Решите уравнение −5 x 2+ 8 x + 4 = 0.

Ответ :____

10. Вычислите координаты точки А .

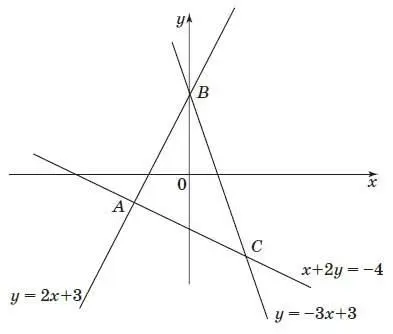
Ответ:____

11. Прочитайте задачу: «Груз массой 30 т предполагалось перевезти одной машиной за несколько рейсов. Однако для перевозки этого груза пришлось использовать машину, грузоподъемность которой на 2 т больше, чем предполагалось. В результате было выполнено на 4 рейса меньше, чем намечалось. За сколько рейсов был перевезен этот груз?»

Выберите уравнение, соответствующее условию задачи, если буквой x обозначена грузоподъемность (в т) машины, с помощью которой планировали перевозить груз.

12. Решите неравенство 1/ 4 х + 1 > 13.

1) х > −48;

2) х > −3;

3) х < −48;

4) х < 3.

13. На рисунке изображен график функции у = х 2−− 4 х + 3. Используя график, решите неравенство х 2+ 3 > 4 х .

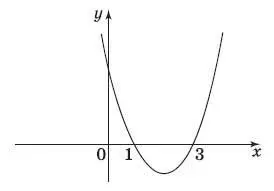
1) (−∞; 1);

2) (−∞; 1)U(3; +∞);

3) (1; 3);

4) (3; +∞).

15. Формула n -го члена геометрической прогрессии имеет вид b n = 5 × 3 n . Какое из данных чисел является членом этой прогрессии?

1) −15;

2) 27;

3) 135;

4) 75.

16. Две группы туристов А и Б отправились в поход по различным маршрутам. На рисунке показаны графики движения этих групп. (По горизонтальной оси откладывается время, прошедшее с начала путешествия – в днях, а по вертикальной – расстояние, пройденное за это время – в километрах.) Сколько километров прошла каждая из групп во второй день своего путешествия?

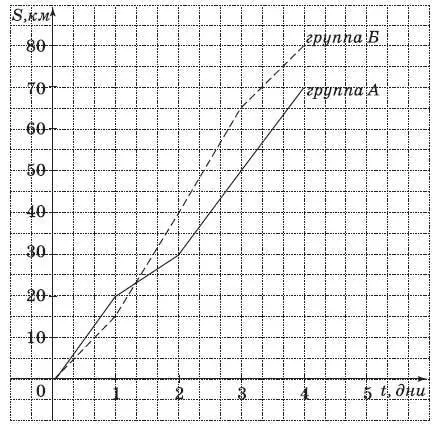
Ответ:______

При выполнении заданий 17–21 используйте отдельный подписанный лист. Сначала укажите номер задания, а затем запишите его решение.

17. Сократите дробь

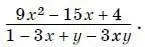
19. Сумма первых девяти членов арифметической прогрессии больше 200, но меньше 220. Найдите разность этой арифметической прогрессии, если известно, что ее первый член равен 8 и все члены этой прогрессии – натуральные числа.