Е. Неискашова - Алгебра. 9 класс. 50 типовых вариантов экзаменационных работ для подготовки к ГИА
- Название:Алгебра. 9 класс. 50 типовых вариантов экзаменационных работ для подготовки к ГИА
- Автор:
- Жанр:
- Издательство:Array Литагент «Аудиокнига»
- Год:2009
- Город:Москва
- ISBN:978-5-17-059843-4,978-5-271-24146-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Е. Неискашова - Алгебра. 9 класс. 50 типовых вариантов экзаменационных работ для подготовки к ГИА краткое содержание
Каждый вариант составлен в полном соответствии с требованиями государственной итоговой аттестации и включает задания разных типов и уровня сложности по всем основным темам, которые выносятся на экзамен: числа, буквенные выражения, преобразования алгебраических выражений, уравнения, неравенства, последовательности и прогрессии, функции и графики.
Значительный по объему банк экзаменационных материалов предоставляет отличную возможность для интенсивной тренировки и овладения необходимыми для успешной сдачи экзамена умениями и навыками.
В конце книги даны ответы для самопроверки на все задания.
Алгебра. 9 класс. 50 типовых вариантов экзаменационных работ для подготовки к ГИА - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
20. Для рытья котлована выделили два экскаватора. После того, как первый проработал 6 часов, его сменил второй, который за 2 часа закончил работу. За какое время выроют котлован оба экскаватора, работая вместе, если известно, что второй экскаватор, работая один, вырыл бы этот котлован на 5 часов быстрее, чем первый?
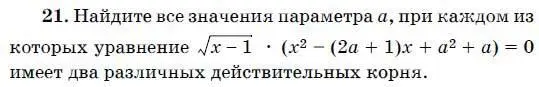
Вариант 9
1. Расположите в порядке убывания числа 0,1237; 0,12; 0,013.
1) 0,1237; 0,12; 0,013;
2) 0,013; 0,12; 0,1237;
3) 0,1237; 0,013; 0,12;
4) 0,12; 0,013; 0,1237.
2. Численность населения Индонезии составляет 2,4 × 10 8человек, а Вьетнама – 8,5 × 10 7человек. Во сколько раз численность населения Индонезии больше численности населения Вьетнама?
1) примерно в 28 раз;
2) примерно в 280 раз;
3) примерно в 2,8 раза;
4) примерно в 3,5 раза.
3. На начало торгов стоимость одной акции фирмы А составляла 1200 руб. К концу дня ее стоимость снизилась на 10 %. В течение следующего дня ее стоимость возросла на 5 %. Какова стоимость одной акции к концу второго дня торгов?
1) 1140 руб.;
2) 1134 руб.;
3) 60 руб.;
4) 1260 руб.
4. Составьте выражение для вычисления стоимости 1 минуты разговора (в руб.) по междугородной связи, если за n часов разговора было заплачено m рублей.

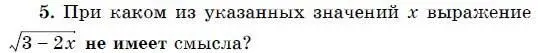
6. В каком случае выражение преобразовано в тождественно равное?
1) 2 x − 2( x − 1) = 2;
2) (3 − x ) 2= 9 − 6 x + x 2;
3) ( x + 2 y )(2 y − x ) = x 2− 4 y 2;
4) ( x + y )( x + y ) = x 2+ y 2.

8. Найдите значение выражения 7√ 3 × 5√ 2 × √6.
Ответ:____
9. Решите уравнение 3 х − 2 = 5 − 7( х − 3).
Ответ:____
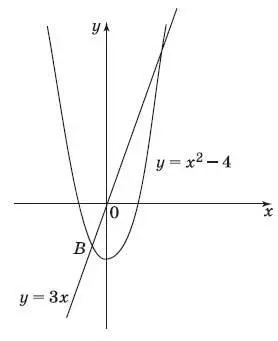
10. На рисунке изображены графики функций
у = х 2− 4 и у = 3 х . Вычислите координаты точки В .
Ответ:____
11. Прочитайте задачу: «Расстояние между двумя пристанями по реке равно 12 км. Лодка проплыла от одной пристани до другой и вернулась обратно, затратив на весь путь 5 часов. Найдите собственную скорость лодки, если скорость течения реки равна 1 км/ч.»
Какое уравнение соответствует условию задачи, если буквой х обозначена собственная скорость лодки (в км/ч)?
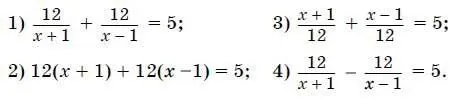
12.Решите неравенство:
− 1/ 3 x + 12 < 0.
1) x < 4;
2) x < −4;
3) x > −36;
4) x > 36.
13. На рисунке изображен график функции y = x 2– 3 x . Используя график, решите неравенство x 2> 3 x .
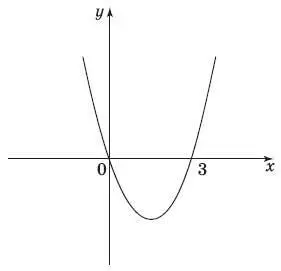
1) (−∞; 0);
2) (3; +∞);
3) (−∞; 0) и (3; +∞);
4) (0; 3).
14. Последовательность задана условиями
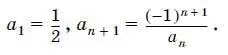
Найдите a 5.
Ответ:____
15. Для каждого графика укажите соответствующую формулу.
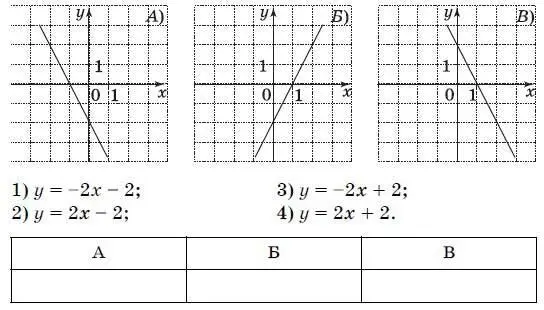
16. В магазин поступили в продажу две новые модели пылесосов – модель А и модель В. На графиках показано, как эти модели продавались в течение года. (По горизонтальной оси откладывается время, прошедшее с начала продаж – в месяцах, а по вертикальной – число пылесосов, проданных за это время – в тыс. шт.) Сколько всего пылесосов этих двух моделей было продано за первые 4 месяца?
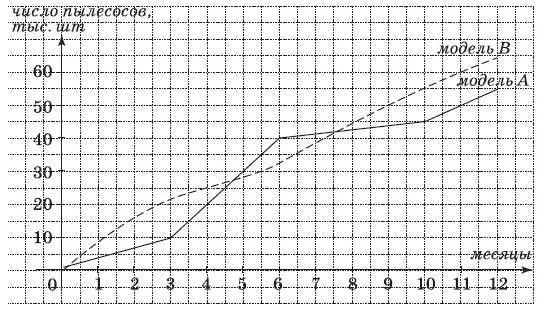
Ответ:____
При выполнении заданий 17–21 используйте отдельный подписанный лист. Сначала укажите номер задания, а затем запишите его решение.
17. Постройте график функции у = 1 − 2 х − 1/ 2 х 2. Укажите наибольшее значение этой функции.
18. Выясните, имеет ли корни уравнение
4 х 2− √3 х = 2 х − 1.
19. Арифметическая прогрессия задана формулой n -го члена a n = 3 n + 2. Найдите сумму членов арифметической прогрессии с 15-го по 50−й включительно.
20. Найдите наименьшее значение выражения
(4 x − 3 y + 2) 2+ (3 x − 2 y + 1) 2и значения x и у , при которых оно достигается.
21. Прямая у = −2 x + b касается окружности x 2+ у 2= 5 в точке с отрицательной абсциссой. Определите координаты точки касания.
Вариант 10
1. За n кг яблок было заплачено m руб. Составьте выражение для вычисления стоимости (в руб.) 100 г яблок.
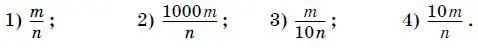

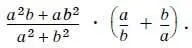
3. Масса Земли равна 5,98 × 10 24кг, а масса Луны – 7,35× 10 22кг. Во сколько раз масса Земли больше массы Луны?
1) примерно в 8,14 раза;
2) примерно в 81,4 раза;
3) примерно в 0,81 раз;
4) примерно в 1,23 раза.
4.Выполните действия 36: 9 − 3× (7 − 5).
1) 12;
2) −2;
3) 3;
4) 2.
5. После снижения цены на 20 % прибор стал стоить 1600 руб. Какова была первоначальная цена этого прибора?
1) 320 руб.;
2) 2000 руб.;
3) 1920 руб.;
4) 400 руб.
6.Упростите выражение
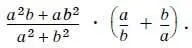
Ответ:________________________
7.Вычислите (1 − √2) 2+ √8.
Ответ:________________________
8.Какое из выражений тождественно равно выражению х 3− 7 х 2+ 12 х ?
1) ( х − 3)( х − 4);
2) х ( х − 3)( х + 4);
3) ( х + 3)( х + 4);
4) х ( х − 3)( х − 4).
9.Решите уравнение
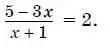
Ответ: _______
10. На рисунке изображены графики функций у = 2 x + 1 и у = 4 − x 2.
Вычислите абсциссу точки А .
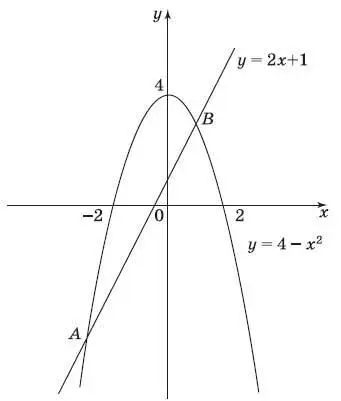
Ответ:__________
Читать дальшеИнтервал:
Закладка:










