Е. Неискашова - Алгебра. 9 класс. 50 типовых вариантов экзаменационных работ для подготовки к ГИА

11. Прочитайте задачу: «Два насоса, работая одновременно, могут выкачать воду из котлована за 2 часа. Один первый насос затратит на эту работу на 3 часа больше, чем один второй насос. За какое время эту работу может выполнить каждый насос, работая отдельно?»

Выберите систему уравнений, не соответствующуюусловию задачи, если буквами x и у обозначены производительности первого и второго насосов соответственно.

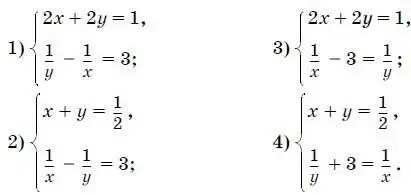
12. Для каждого неравенства укажите множество его решений.

А) x 2− 4 x > 0; Б) x 2+ 4 x ≤ 0; В) 4 x − x 2> 0.

1) (−∞; +∞);

2) (−∞; 0)U(4; +∞);

3) [−4; 0];

4) (0; 4).

13. Какое из приведенных ниже неравенств не следует из неравенства x − у < z + 1?

1) x − z < у + 1;

2) x − 1 < у + z ;

3) z − у < x + 1;

4) у + z > x − 1.

14. Члены последовательности можно изображать точками на координатной плоскости. Для этого по горизонтальной оси откладывают номер члена, а по вертикальной – соответствующий член последовательности. На рисунке изображены точками первые шесть членов арифметической прогрессии a n . Найдите a 1, d .

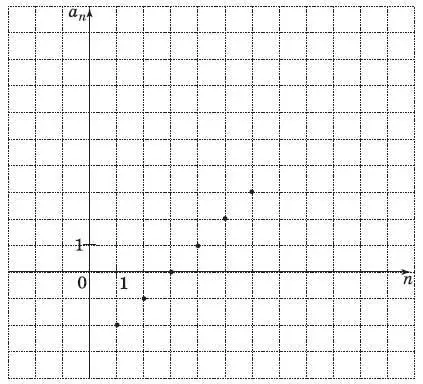
Ответ:__________

15. Какая из данных прямых не имеет общих точек с графиком функции

у = 1/ x + 1?

1) у = 0;

2) у = 1;

3) у = −2;

4) х = 1.

16. Две группы туристов – А и Б – отправились в поход по различным маршрутам. На рисунке изображены графики движения этих групп. (По горизонтальной оси откладывается время, прошедшее с момента начала движения – в днях, а по вертикальной – расстояние, пройденное за это время – в км.) Какая из туристических групп прошла за третий день путешествия большее расстояние, и на сколько?

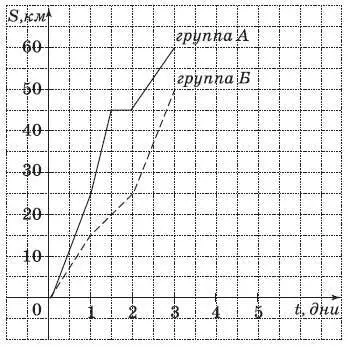
Ответ:________

При выполнении заданий 17–21 используйте отдельный подписанный лист. Сначала укажите номер задания, а затем запишите его решение.

17. Постройте график функции

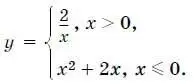
Найдите наименьшее значение функции.

18. Решите уравнение

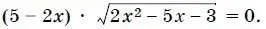
19. Найдите сумму всех двузначных натуральных чисел, не кратных 13.

20. Расстояние между городами равно 840 км. Одновременно навстречу друг другу из них выходят два поезда, которые встречаются через 7 часов. Если бы один из поездов вышел на 2 ч 30 мин раньше, то поезда встретились бы через 6 часов после выхода второго поезда. Определите скорость каждого поезда, зная, что поезда двигались с постоянными скоростями.

21. Найдите все значения параметра а , при каждом из которых меньший корень уравнения

x 2− (2 a − 1) x + a 2− a = 0

удовлетворяет неравенству 2 x 2+ x − 10 < 0.

1. Найдите значение выражения

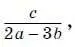
если а = − 1,8, b = − 0,4, c = 4,8.

1) 2;

2) −1;

3) −2;

4) 1.

2.Запишите выражение для нахождения стоимости n мин разговора (в руб.) по междугородной связи, зная, что 1 мин разговора стоит m копеек.

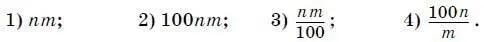
3. Одна из точек, отмеченных на числовой прямой, соответствует числу √45. Какая это точка?

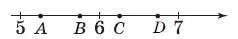
4. Представьте выражение

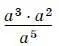
в виде степени с основанием а .

1) 1;

2) а ;

3) а −1;

4) а 4.

5. Каждому покупателю, сделавшему в некотором магазине покупку в период с 8 00до 11 00, предоставляется скидка 5 %. Покупатель, совершивший покупку в этом магазине в указанный период времени, заплатил в кассе за приобретенный товар 741 руб. Сколько рублей покупатель заплатил бы за такой же товар, если бы он приобрел его в этом же магазине в 12 15?

1) 1482 руб.;

2) 703 руб. 95 коп.;

3) 780 руб.;

4) 778 руб. 05 коп.

6. Какое из выражений является тождественно равным произведению

b (2 b − 4) − 2(3 − 2 b )?

1) 2 b 2− 8 b − 6;

2) 3 b − 6;

3) 2 b 2− 6;

4) 2 b 2+ 6.

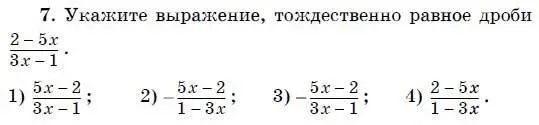
8. Вычислите √84 − (√7+ √3) 2

Ответ:___

9. Найдите координаты точки В

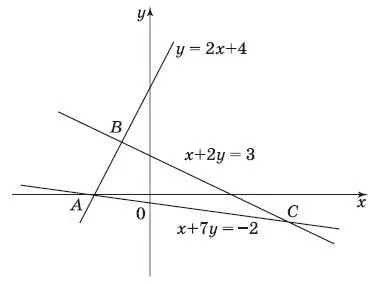
Ответ:___

10. Решите уравнение 7 х 2− 4 х − 3 = 0.

Ответ:____

11. Прочитайте задачу: «Расстояние по реке между пунктами А и В равно 41 км. Из пункта А в пункт В по течению плывет моторная лодка, собственная скорость которой равна 18 км/ч, а из пункта В в пункт А движется вторая моторная лодка, собственная скорость которой равна 16 км/ч. При встрече оказалось, что первая лодка плыла 1 ч, а вторая – 1,5 ч. Найдите скорость течения реки.»

Выберите уравнение, соответствующее условию задачи, если буквой х обозначена скорость (в км/ч) течения реки.

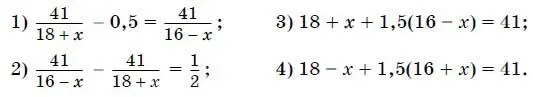
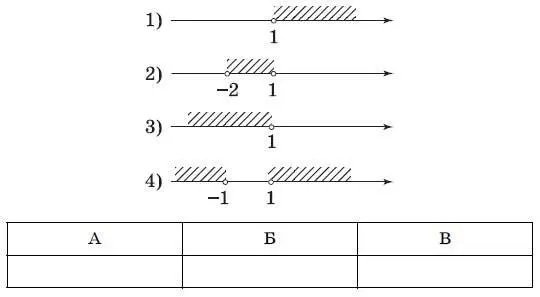
12. Для каждого из приведенных неравенств укажите номер рисунка, на котором изображено множество его решений.

A) x > 2 x − 1; Б) x 2− x < 0; В) x 2− 1 > 0.

13. Какое из приведенных ниже неравенств не следует из неравенства 2 x − 3 ≤ 9 + 5 x ?

1) −3 x − 12 ≤ 0;

2) x + 4 >= 0;

3) x >= 4;

4) 4 − x ≤ 0.

14. Какая из данных прямых не имеет общих точек с параболой y = 2 x − x 2?

1) у = 0;

2) x = 0;

3) y = 5;

4) y = −1.