Е. Неискашова - Алгебра. 9 класс. 50 типовых вариантов экзаменационных работ для подготовки к ГИА

1) √3;

2) √1800;

3) √3600;

4) ни одно из этих чисел.

3. Туристы прошли 75 % от всего туристического маршрута, и им еще осталось пройти 5 км. Какова длина всего маршрута?

1) 3,75 км;

2) 20 км;

3) 15 км;

4) 2 км.

4. Найдите значение выражения

3,5(2 х − 1) − 1,4 × (5х + 2) при х = 11 2/ 33.

1) −6,3;

2) −0,7;

3) 0,7;

4) 6,3.

5. Составьте выражение для нахождения периметра (в см) равнобедренного треугольника, если известно, что длина его основания равна n см, а длина боковой стороны равна m см.

1) n + m ;

2) n + 2 m ;

3) 2 n + m ;

4) n × m .

6. В каком случае выражение преобразовано в тождественно равное?

1) 2( х + у ) = 2 х + у ;

2) ( х + у ) 2− ( х − у ) 2= 4 ху ;

3) ( х + у ) 2+ ( х − у ) 2= х 2+ у 2;

4) ( х − у ) 2− 2 ху = х 2+ у 2.

8. Найдите частное

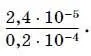
Ответ запишите в виде десятичной дроби.

Ответ:____

9. Решите уравнение 3 − 2 x = 6 x − 4( x − 2).

Ответ:____

10. Прямая y = 2 х + 1 пересекает параболу y = − x 2+ 9 в двух точках. Вычислите координаты точки А .

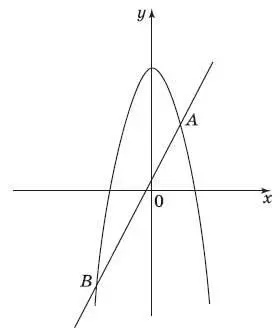
Ответ:____

11. Прочитайте задачу: «Расстояние от пункта А до пункта В автомобиль проезжает с определенной скоростью за 2,5 часа. Если увеличить скорость этого автомобиля на 20 км/ч, то он за 2 часа проедет расстояние, которое на 15 км больше расстояния от пункта А до пункта В . Найдите расстояние между пунктами А и В .»

Выберите уравнение, соответствующее условию задачи, если буквой х обозначена скорость (в км/ч) автомобиля.

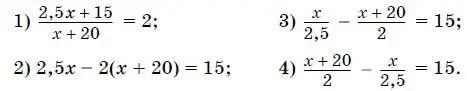
12. Решите неравенство 3 х − 4(2 х − 3) ≤ 13.

1) х ≤ −0,2;

2) х ≤ −5;

3) х >= −0,2;

4) х >= −5.

13. На рисунке изображен график функции у = 2 х 2− 6 х . Используя график, решите неравенство 2 х 2− 6 х < 0.

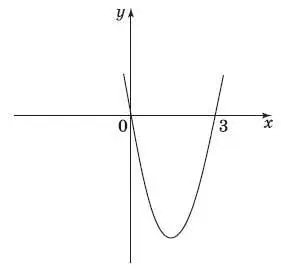
1) (−∞; 0);

2) (0; 3);

3) (3; +∞);

4) (−∞; 0)U(3; +∞).

14. Для каждой арифметической прогрессии, заданной a 1и d , укажите формулу ее n -го члена. (В таблице под каждой буквой запишите номер ответа, под которым указана соответствующая формула n -го члена арифметической прогрессии.)

А) a 1= 2, d = 3; Б) a 1= 3, d = 2; В) a 1= 1, d = 2.

1) a n = 3 n + 2;

2) a n = 3 n − 1;

3) a n = 2 n + 1;

4) a n = 2 n − 1.

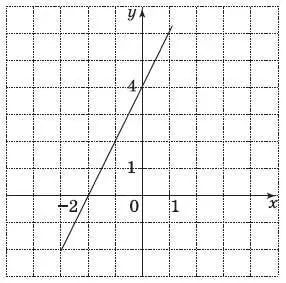
15. График какой линейной функции изображен на рисунке?

1) y = −2 x + 4;

2) y = 2 х + 4;

3) y = 4 х − 2;

4) y = 4 х + 2.

16. В продажу выпустили новую модель телефона. На графиках показано, как эта модель продавалась в течение года в магазинах двух фирм сотовой связи А и В. (По горизонтальной оси откладывается время, прошедшее с начала продаж – в месяцах, а по вертикальной – число телефонов, проданных за это время – в тыс. шт.) Определите, сколько телефонов было продано за первые три месяца с начала продаж.

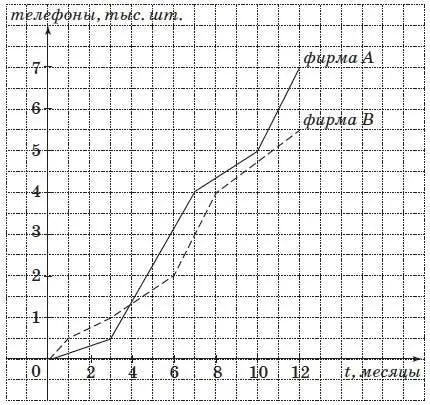
Ответ:____

При выполнении заданий 17–21 используйте отдельный подписанный лист. Сначала укажите номер задания, а затем запишите его решение.

17. Найдите область определения функции

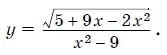
18. Найдите значение выражения

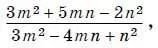
если известно, что

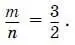
19. Решите систему уравнений

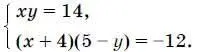
20. За пять дней совместной работы два рабочих выполнили 11/ 18всего задания. Оставшуюся часть задания первый рабочий выполнил за 7 дней. За сколько дней может выполнить все задание второй рабочий, работая один?

21. Найдите все значения параметра а, при каждом из которых график функции у = | х 2− 2( а − 2) х + а 2− 4 а + 3 | пересекает прямую у = а 2+ 3 а − 3 в трех различных точках.

1. Население Италии составляет 6 × 10 7человек, а ее территория равна 3,01 × 10 5км. Какой из приведенных ответов характеризует среднее число жителей на 1 км 2?

1) 199 чел.;

2) 1,99 × 10 3чел.;

3) 5 чел.;

4) 0,5 × 10 2чел.

2. Зерна кофе при обжарке теряют 12 % своего веса. Сколько килограммов жареного кофе получится из 5 кг свежего?

1) 4,4 кг;

2) 0,6 кг;

3) 6 кг;

4) 0,44 кг.

3. Укажите наименьшее из чисел 6/ 13.; 3/ 7; 0,5; 0,402.

1) 6/ 13;

2) 3/ 7;

3) 0,5;

4) 0,402.

4. Найдите значение выражения a / ( b + c ) при a = 0,8, b = −0,7, c = 0,3.

1) −0,8;

2) −2;

3) 0,8;

4) 2.

5. Зная длину своего шага, человек может рассчитать пройденное им расстояние s по формуле s = nl , где n – число шагов, l – длина шага. Какое расстояние прошел человек, сделавший 2800 шагов, если длина его шага составляет примерно 55 см? Ответ выразите в километрах.

Ответ:____

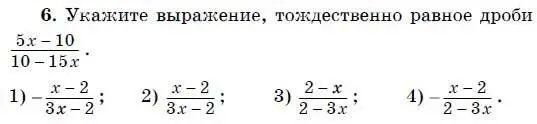
7. В какой многочлен можно преобразовать выражение

−4( х + 2) + ( х − 4) 2?

1) 8 − х 2;

2) 8 − 12 х + х 2;

3) 24 − 6 х + х 2;

4) −4 − 2 х + х 2.

8. Найдите значение выражения (3√2) 2− (2√3) 2.

Ответ:____

9. Решите уравнение 4 х 2− 9 х − 9 = 0.

Ответ:___

10. Вычислите координаты точки А .