Фрэнк Фабоцци - Рынок облигаций. Анализ и стратегии

В главе 2 мы писали о том, почему цена облигации, не имеющей встроенных опционов, может быть выражена в виде формулы [18] Формула (4.1) предполагает, что следующая купонная выплата состоится ровно через шесть месяцев с настоящего времени и накопленный купонный доход отсутствует. Как мы уже объясняли в главе 2, данную модель несложно приспособить к ситуации, когда купонная выплата ожидается менее чем через шесть месяцев: цена должна быть уточнена с поправкой на накопленный купонный доход. :

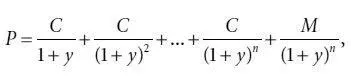(4.1)

где:

P – цена облигации;

C – полугодовая купонная выплата (в долларах);

y – половина доходности к погашению или требуемой доходности;

n – число полугодовых периодов (число лет × 2);

M – номинальная стоимость (в долларах).

Для выяснения примерного изменения цены при небольшом изменении доходности следует вычислить первую производную выражения (4.1) по требуемой доходности:

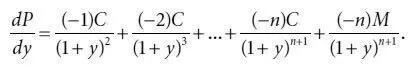(4.2)

Преобразовав формулу (4.2), получаем:

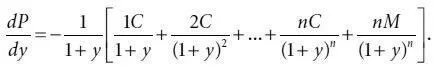(4.3)

Выражение в скобках – это средневзвешенный срок до погашения денежных потоков облигации (взвешивание производится по приведенной стоимости денежного потока).

Формула (4.3) обозначает приблизительное долларовое изменение цены при небольшом изменении требуемой доходности. Деление обеих частей выражения (4.3) на Р позволяет найти значение примерного процентного изменения:

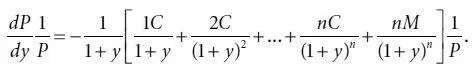(4.4)

Выражение в скобках, деленное на цену (в нашем случае умноженное на 1/ Р ), принято называть дюрацией Маколея [19] Фредерик Маколей впервые ввел этот термин в исследовании, опубликованном в 1938 году Национальным бюро экономических исследований: данная мера была использована вместо срока до погашения для обозначения приблизительного значения средней продолжительности времени, в течение которого инвестиция в облигацию находится в обращении (см. Frederick Macaulay, S ome Theoretical Problems Suggested by the Movement of Interest Rates, Bond Yields, and Stock Prices in the U.S. Since 1856 (New York: National Bureau of Economic Research, 1938)). Исследуя чувствительность финансовых учреждений к изменению процентных ставок, Редингтон и Сэмюэльсон, независимо друг от друга, также пришли к осознанию необходимости введения меры дюрации (см. F. M. Redington, «Review of the Principle of Life Office Valuation», Journal of the Institute of Actuaries , 1952, pp. 286–340; и Paul A. Samuelson, «The Effect of Interest Rates Increases on the Banking System», American Economic Review , March 1945, pp. 16–27). , таким образом:

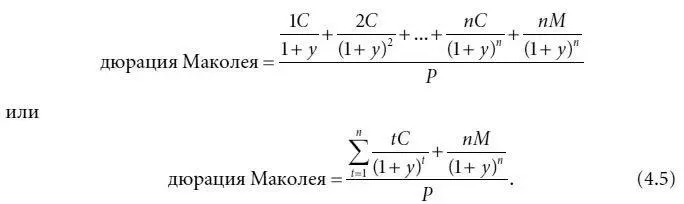
Подставив величину дюрации Маколея в формулу (4.4) для вычисления примерных процентных изменений цены, получим:

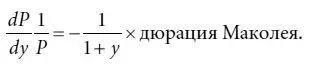(4.6)

Отношение дюрации Маколея к 1 + у получило название модифицированной дюрации. Таким образом:

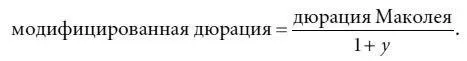(4.7)

Подставив выражение (4.7) в формулу (4.6), получим:

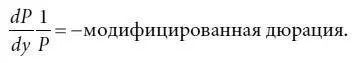(4.8)

Из формулы (4.8) видно, что модифицированная дюрация связана с примерным процентным изменением цены при данном изменении доходности. Поскольку для всех облигаций без встроенных опционов модифицированная дюрация является положительным числом, выражение (4.8) устанавливает обратную зависимость между модифицированной дюрацией и примерным процентным изменением цены при данном изменении доходности. Это закономерный результат: как известно, фундаментальный принцип движения цен на облигации гласит, что они изменяются в направлении, противоположном направлению движения процентных ставок.

В табл. 4.4 и 4.5 приводятся данные о дюрациях Маколея и модифицированных дюрациях двух пятилетних купонных облигаций. Дюрации выражены в количестве периодов (а не лет). Таким образом, мы имеем дело с полугодовой дюрацией: денежные потоки данных облигаций поступают раз в полгода. Для получения значений годовой дюрации, приведенные значения следует поделить на 2 (см. примечания к табл. 4.4 и 4.5). Заметим, что при поступлении денежного потока m раз в году дюрация, выраженная в годах, уточняется путем деления на m , т. е.:

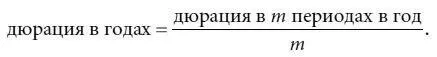
Дюрация Маколея в годах и модифицированная дюрация для шести гипотетических облигаций равны:

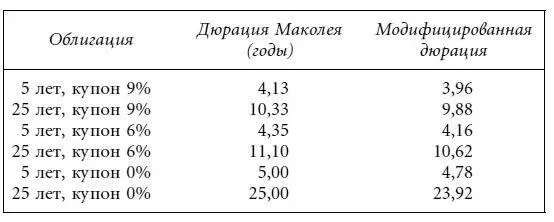
Вместо того чтобы использовать выражение (4.5) для вычисления дюрации Маколея и формулу (4.7) для получения модифицированной дюрации, мы предлагаем разработать альтернативное выражение, не требующее кропотливых вычислений, предполагаемых формулой (4.5). Цену облигации мы выразим в терминах следующих двух компонентов: 1) приведенная стоимость аннуитета, где аннуитет – это сумма купонных выплат; и 2) приведенная стоимость номинала. Таким образом, цена облигации номинальной стоимостью $100 будет равна [20] Первое выражение в скобках в формуле (4.9) – это приведенная стоимость купонных выплат из формулы (2.7), дисконтированная по у . :

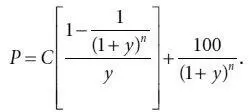(4.9)

Взяв первую производную выражения (4.9) и поделив результат на Р , получим новую формулу вычисления модифицированной дюрации:

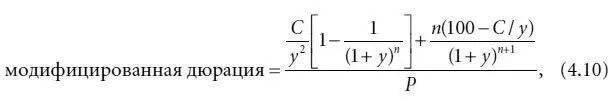
где цена выражена в виде процента номинальной стоимости. Дюрация Маколея может быть получена посредством умножения выражения (4.10) на (1 + у ). В качестве иллюстрации рассмотрим 25-летнюю 6 %-ную облигацию, торгующуюся по 70,357 при доходности 9 %. В этом случае:

Подставим имеющиеся значения в формулу (4.10) и получим:

Переведем значение в годы: поделим результат на 2 и получим 10,62 – модифицированную дюрацию. Умножим на 1,045 и получим 11,10 – дюрацию Маколея.