Фрэнк Фабоцци - Рынок облигаций. Анализ и стратегии

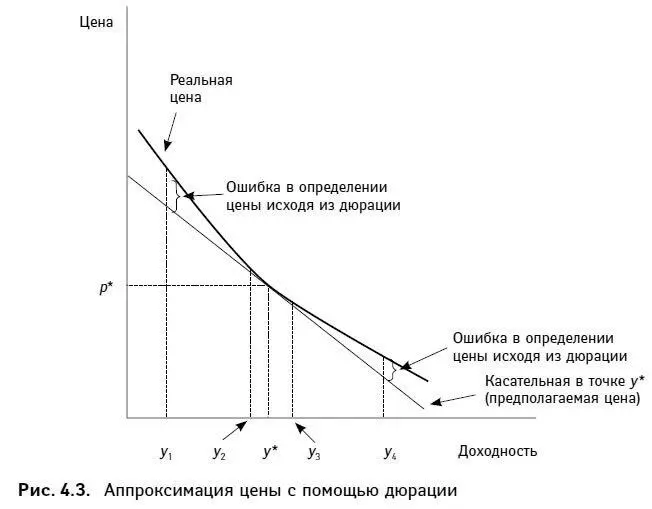
Обратим внимание на поведение дюрации (крутизны наклона касательной) при изменении доходности: при росте (падении) доходности, дюрация падает (растет). Это свойство, как мы отмечали ранее, характерно для облигаций без встроенных опционов.

Проведем, как это показано на рис. 4.3, вертикальную линию из любой точки доходности (на горизонтальной оси): расстояние между горизонтальной осью и касательной – это цена, аппроксимированная путем использования дюрации при начальной доходности у *. Аппроксимированный результат будет меньше реальной цены – феномен, который мы уже наблюдали, говоря об отношениях между дюрацией (касательной) и аппроксимированным ценовым изменением. При падении доходности предполагаемое изменение цены меньше реального – реальная цена, таким образом, недооценивается. И наоборот: если доходность растет, предполагаемое значение изменения цены будет больше, чем значение реального изменения – реальная цена опять окажется недооценена.

При небольших изменениях доходности линия касательной и дюрация дают хорошую аппроксимацию реальной цены. В то же время, чем дальше от точки начальной доходности у *, тем хуже аппроксимация. Очевидно, что точность аппроксимации непосредственно связана с выпуклостью кривой, отражающей зависимость цена – доходность облигации.

Дюрация (модифицированная или долларовая) предполагает описание выпуклой функции с помощью прямой линии (касательной). Возможно ли найти математическую формулу, обеспечивающую лучшую аппроксимацию изменений цены на облигацию при изменении требуемой доходности?

Попробуем применить первые два члена ряда Тейлора и аппроксимировать ценовые изменения следующим образом [23] Ряд Тейлора, описание которого можно найти в учебниках по математическому анализу, используется для аппроксимации функций. В данном случае аппроксимируемой функцией является зависимость цены от доходности. :

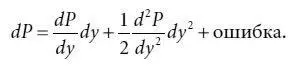(4.15)

Делим обе части равенства (4.15) на Р и получаем процентное изменение цены:

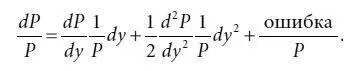(4.16)

Первый член правой части равенства (4.15) – это выражение (4.14), т. е. долларовое изменение цены, измеренное на основе долларовой дюрации. Таким образом, первый член в выражении (4.15) – искомая аппроксимация абсолютных ценовых изменений на основе дюрации. В выражении (4.16) первый член правой части равенства – аппроксимация процентных изменений цены на основе модифицированной дюрации.

Вторые члены выражений (4.15) и (4.16) включают вторую производную функции цены (уравнения (4.1)). Это та самая вторая производная, которую мы используем в качестве поправки для учета влияния выпуклости зависимости цена – доходность. Вторую производную цены принято называть долларовой мерой выпуклости облигации.Итак:

(4.17)

Произведение долларовой меры выпуклости и квадрата изменения требуемой доходности является предполагаемым ценовым изменением, обусловленным выпуклостью. Таким образом, аппроксимированное изменение цены, обусловленное выпуклостью, равно:

Вторая производная, поделенная на цену, – это мера процентного изменения цены облигации, обусловленного выпуклостью; ее называют просто мерой выпуклости. Итак:

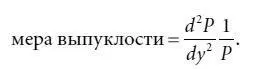(4.19)

А процентное изменение цены, обусловленное выпуклостью, равно:

(4.20)

Вторая производная цены как функции доходности, выраженной согласно формуле (4.1), равна:

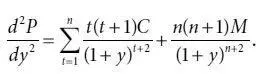(4.21)

В табл. 4.7 и 4.8 приведены значения второй производной [формула (4.21)], годовой долларовой меры выпуклости и годовой меры выпуклости для двух пятилетних купонных облигаций. Мера выпуклости выражена в квадратах периодов. Для перевода меры выпуклости в годы следует поделить выражения (4.17) и (4.19) на 4 (т. е. 22). Таким образом, если денежный поток поступает m раз в году, выпуклость выражается в годах следующим образом:

Годовая долларовая мера выпуклости и годовая мера выпуклости для наших шести гипотетических облигаций выглядят следующим образом:

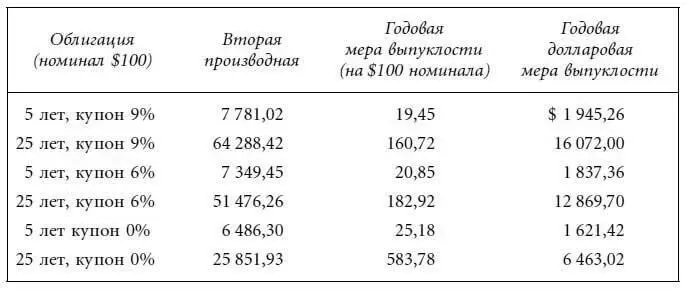
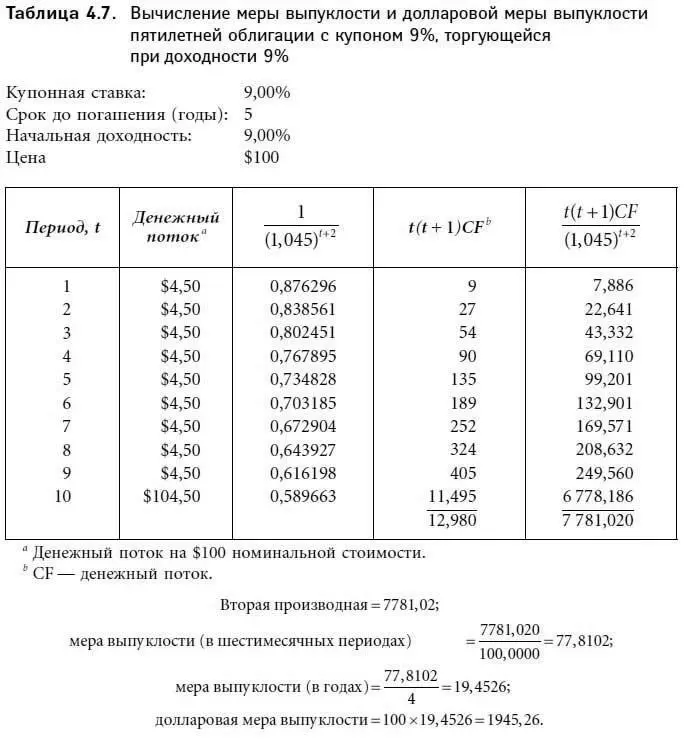
Вторая производная может быть также получена путем взятия второй призводной от выражения (4.9). Таким образом, мы можем упростить выражение (4.21):

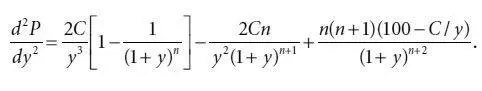(4.22)

В качестве примера использования формулы (4.22) рассмотрим 25-летнюю облигацию с купоном 6 %, торгующуюся по 70,357 при доходности 9 %. Вторая производная равна:

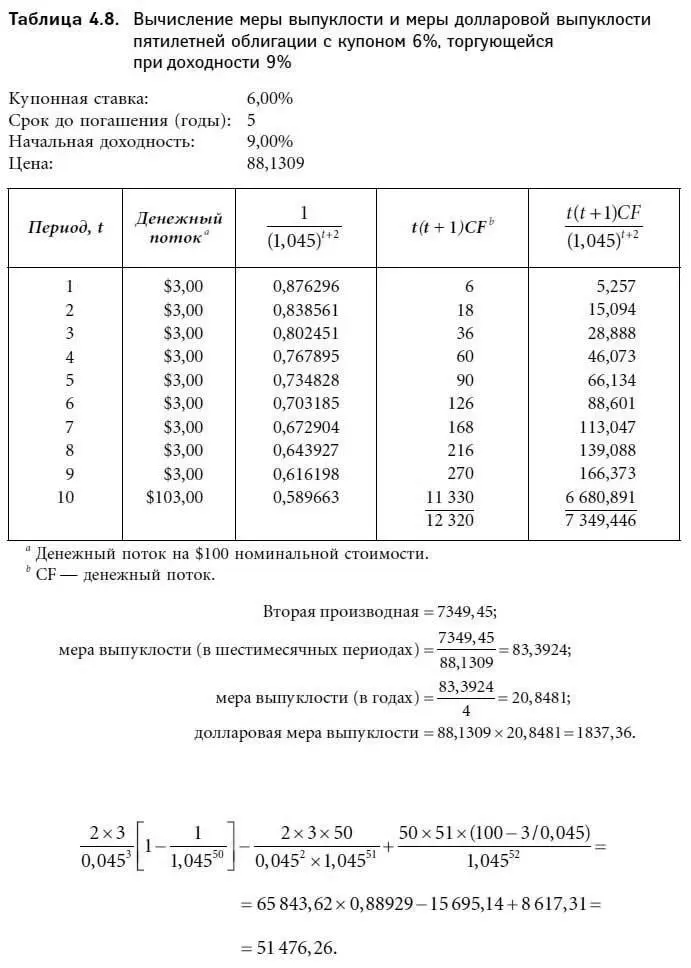
Обратите внимание на то, что полученное значение совпадает с результатом, найденным ранее.

Из формулы (4.16) видно, что значение процентного изменения цены облигации может быть найдено с учетом двух величин: дюрации и меры выпуклости. Рассмотрим в качестве примера 25-летнюю облигацию с купоном 6 %, торгующуюся при доходности 9 %. Модифицированная дюрация облигации составляет 10,62, а мера выпуклости равна 182,92. Если требуемая доходность возрастет на 200 базисных пунктов – с 9 % до 11 %, то аппроксимированное процентное изменение цены облигации может быть получено следующим образом:

процентное изменение цены, обусловленное выпуклостью, по формуле (4.20) =