Коллектив авторов - Новые головоломки Шерлока Холмса

10 на 20 дюймов. Обычно прямоугольный предмет с максимальной плотностью – это квадрат. Но, поскольку верхняя и нижняя рамки вдвое шире левой и правой, высота картины должна быть вдвое больше ширины, чтобы незадействованное пространство оказалось минимальным. Таким образом, холст должен быть 20 дюймов в высоту и 10 в ширину, а сама картина – 12 дюймов в высоту и 6 в ширину.

Кому-то из вас, друзья, задача показалась легкой; если же нет, то крепче держитесь за кресла. Задача очень прямолинейная, но решается в несколько этапов.

Нам известно, что 95x+97y = 4238; количество и свиней, и овец должно быть целым и больше нуля. Решить задачу нам позволит теория неопределенных уравнений. Сначала решим наше уравнение для x: x = 4238/95-97y/95; сведем это выражение к целым числам и остаткам: x = 44+58/95-y-2y/95.

Упрощая, получаем: x = 44-y+(58-2y)/95.

Поскольку x – целое число, правая сторона уравнения тоже должна быть целым числом. И 44, и y – целые числа, так что последний член, (58-2y)/95 – тоже целое число, хотя мы совершенно не представляем, что это за число. Давайте для простоты обозначим его «2i». Решим новое определение 2i = (58-2y)/95 по y: y = 29-95i. Нам известно, что y – неотрицательное целое число, так что 0 ≤ 29-95i, а i ≤ 29/95.

Теперь у нас есть выражение для y, которое мы можем подставить в исходное уравнение для x: x = 44-(29-95i)+(58-2(29-95i))/95; выглядит все не то чтобы очень красиво, но многое здесь сокращается, и после всех упрощений мы получаем x = 4-29+95i+2i, или x = 15+97i. Поскольку x – целое число, получается, что 0 ≤ 15+97i, а -15/97 ≤ i.

Итак, i находится в промежутке -15/97 ≤ i ≤ 29/95; поскольку i при этом – целое число, оно может быть только нулем.

Выражаем и x, и y через i: x = 15+97×0, или 15; y = 29–95×0, или 29. За x мы приняли число свиней, так что он купил 15 свиней. С помощью этого метода можно решить любое неопределенное уравнение; впрочем, чем больше в уравнении неизвестных, тем больше шагов вам понадобится. Если уравнение нерешаемо, то промежуток, полученный для i, будет невозможным.

Три слова: плутовство, шарлатанка, ограбление. Общая тема – преступная деятельность.

Джентльмен покупал медные цифры. Он собирался прикрепить их к двери, чтобы номер его дома был хорошо виден с улицы.

Возьмите десять спичек и выложите из них слово FIVE («пять»). Затем уберите семь из десяти спичек, оставив только IV – римскую 4. Очень просто, если знать способ решения, – но все загадки таковы.

3 и 5; 7 и 8. Чтобы решить задачу математически, придется добавить неопределенности. Мы знаем, что x 2+xy+y 2равно квадратному числу. Это квадратное число мы можем выразить в виде (x – ay) 2, поскольку оно всегда будет точным квадратом, а переменный коэффициент a позволит нам получить нужное число при любых x и y.

Теперь разложим это квадратное выражение: (x – ay) 2= (x – ay)(x – ay) = x 2-2axy+a 2y 2. Отсюда видно, что x+y = ya 2-2ax. Прибавим к обеим сторонам 2ax – y, и получим x+2ax = ya 2—y, или x(2a+1) = y(a 2-1).

Поскольку мы знаем, что xy = yx, отсюда следует, что x = a 2-1, а y = 2a+1. Если a = 1, то x = 0, y = 2; решение вполне верное, но нам нужны целые числа от 1 до 9. a = 2 дает нам x = 3, y = 5, а a = 3 дает x = 8, y = 7. Если a = 4, то x > 9.

Я лично, впрочем, решил задачу перебором.

В 10 футах (около 3 метров) под землей температура почвы отстает примерно на четыре месяца от температуры воздуха, по крайней мере, в средней полосе. Когда на поверхности Земли заканчивается весна, у кротов и червей еще продолжается зима. На глубине больше 75 футов времена года вообще никак не ощущаются – по крайней мере, у нас в Лондоне.

200 километров. Возьмем за x расстояние от места, где начались проблемы с локомотивом, до места назначения, а за y – полную скорость. Нам известно следующее: нормальное время t, за которое мы должны были добраться до места назначения, равно x/y; на скорости (3/5)y время равно t+2 = 5x/3y; наконец, если бы мы проехали еще 50 километров, то опоздали бы всего на 1 час 20 минут: t+4/3 = 50/y+5(x-50)/3y. Вычтите из второго уравнения t = x/y, и быстро обнаружите, что t = 3, а x = 3y.

Итак, если бы все было в порядке, нам бы оставалось ехать 3 часа, а оставшееся расстояние равняется 3, умноженным на максимальную скорость поезда в километрах в час. Мы знаем, что по третьему уравнению добрались бы до места назначения на 2/3 часа быстрее, чем по второму; подставим в третье уравнение t+2 = 5x/3y, и получим 5x/3y-2/3 = 50/y+5x/3y-250/3y; 5x-2y = 150+5x-50; 2y = 100. Таким образом, полная скорость равна 50 км/ч. Чтобы преодолеть расстояние на полной скорости, требуется 4 часа, так что оно равно 200 км.

28. Начните с конца и продвигайтесь к началу, и все будет очень просто.

2×10 = 20. 20-8 = 12. 12×12 = 144. 144+52 = 196. 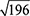= 14. 14×3:2 = 21. 21×7 = 147. 147×4:7 = 84. 84:3 = 28. Заметим, что выражение «×4:7» обратно «+75 %», потому что 4/4+3/4 = 7/4.

На самом деле – да. Помните: отсчет времени начинается с первого выстрела, так что время t в этот момент равняется 0 секундам, а не 5. Чтобы винтовка полностью соответствовала хвастливым заявлениям Морана, нужно, чтобы она делала 60 выстрелов за 4 минуты 55 секунд. Другая иллюстрация того же принципа: поставив на бумаге две точки, вы соединяете их одной линией, а не двумя.

Три слова: провокация, беспорядки, задержание.

2 полукроны. Мы знаем, что и Уиггинс, и Барнабас прикладывают одинаковые усилия и для одной, и для другой работы. Уиггинс выбрасывает грязь так же быстро, как Барнабас копает, но копает вчетверо быстрее, чем Барнабас выбрасывает грязь. Чтобы непосредственно сравнить, с какой скоростью копают Уиггинс и Барнабас, нужно два шага, но, поскольку они оба и для копания, и для выбрасывания грязи прикладывают одинаковые усилия, получается, что в целом Уиггинс работает вдвое эффективнее Барнабаса. Итак, как бы они ни разделяли работу между собой и сколько бы времени ни потратили, Уиггинс работал в два раза лучше Барнабаса, и деньги нужно разделить в соотношении 2:1.

20 и 64. Два числа, произведение которых равно 1280, а разность – 44, можно найти простым подбором, но есть и алгебраическое решение.

Мы знаем, что xy = 1280, а x – y = 44. Итак, x = 44+y. После подстановки получаем 44y+y2 = 1280; представим это в виде стандартного квадратного уравнения: y2+44y-1280 = 0.

Формула для решения квадратного уравнения имеет вид 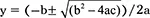, где a, b и c – коэффициенты при соответствующих членах квадратного уравнения. Знак ± означает, что решать нужно дважды: в первый раз – прибавить квадратный корень, во второй – отнять. В нашем случае a = 1, b = 44, c = -1280.