Айзек Азимов - Числа: от арифметики до высшей математики

А теперь представьте себе, что надо на счетах сложить семь и восемь. Как ни странно, это даже трудней, чем получить сумму от сложения нескольких сотен тысяч, что мы только что сделали.

Посмотрите на рисунок.

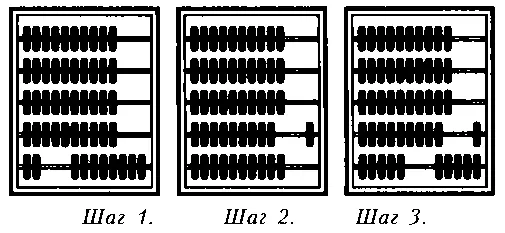
Сначала на нижнем ряду вы переводите направо восемь костяшек. Теперь нужно к ним прибавить еще семь, но у нас на нижнем ряду свободны только две костяшки. Что же делать? Все очень просто. Сначала передвигайте оставшиеся две. Теперь у вас есть целый десяток. Вы делаете замену, десять костяшек на нижнем ряду заменяете на одну костяшку на следующем ряду, то есть откладываете в ряду десятков один десяток. Теперь вы можете закончить сложение, ведь ряд единиц у вас свободен. Нам нужно было передвинуть семь костяшек. Две мы уже передвинули. Значит, осталось передвинуть еще пять. Передвигаем пять костяшек на нижнем ряду влево и получаем результат: один десяток и пять единиц, то есть пятнадцать.

Такая замена десяти костяшек на одну в следующем верхнем ряду годится для всех рядов. Десять десятков можно заменить на одну сотню, десять сотен на одну тысячу и так далее.

Таким образом, когда мы используем счеты, нам не надо отсчитывать больше десяти костяшек. На самом деле достаточно считать до пяти. Ведь если вы передвинули направо больше пяти костяшек, нужно только подсчитать количество костяшек в левой части, их всегда будет меньше пяти, чтобы узнать, сколько их в правой части. Скажем, если слева осталась одна костяшка, значит, справа их девять.

Когда костяшек пять или меньше, нам легко определить их количество с первого взгляда, не считая. Поэтому опытный работник, которому приходилось постоянно считать на счетах, мог производить операции сложения и вычитания с большой скоростью, гораздо быстрее, чем это делается по обычной методике, на бумаге, складывая и вычитая в столбик. Самым выдающимся специалистам по работе со счетами удавалось даже обогнать электрические настольные счетные машины.

Используя счеты, вы легко можете показать, что от перемены мест слагаемых сумма не меняется. Неважно, какое число вы первым выставили на счетах. Вы можете сначала отложить семь, а потом восемь, или наоборот, сумма останется той же самой. Это пятнадцать. Так что запомните это правило хорошенько: от перемены мест слагаемых сумма не меняется.

Итак, мы выяснили, какая полезная и удобная вещь — счеты. Но ведь результаты вычислений надо как-то записывать. И в Древнем Вавилоне, и в Древнем Египте велись систематические записи налогов, податей, запасов, поступивших в закрома правителей, и многого другого. Конечно, можно записывать числа словами, как это сделано в начале главы, например двести пятьдесят три тысячи сто двенадцать. Такую запись можно было сделать на любом языке, но это довольно утомительно и неудобно. На помощь пришли сокращения и обозначения.

Уже в древности писцы использовали различные знаки, символы и буквы алфавита для записи чисел. Мы с вами рассмотрим систему буквенных изображений чисел, которую использовали древние римляне. Она используется до сих пор. Римские цифры мы можем увидеть на памятниках, на общественных зданиях, на циферблатах часов, в дипломах и юбилейных грамотах, так что они всем нам хорошо знакомы.

Число один в римской системе обозначалось как I, два — II, три — III, четыре — IIII, пять — V(возможно, это схематичное изображение ладони с отведенным в сторону большим пальцем), шесть — VI, семь — VII, восемь — VIII, девять — VIIII, десять — X(возможно, этот значок обозначал две ладони с отведенными большими пальцами, одну с пальцами, направленными вверх, другую — с пальцами вниз). Дальше идет пятьдесят — L, сто — С, пятьсот — D, тысяча — М.

Так число тысяча девятьсот пятьдесят восемь в римской системе записи будет выглядеть как MDCCCCLVIII(то есть одна тысяча + пятьсот + сто + сто + сто + сто + пятьдесят + пять + один + один + один).

Обратите внимание, в римской системе записи чисел определенный символ всегда обозначал одно и то же число, независимо от того места в строке, которое он занимал. Скажем, вместо MDCCCCLVIIIможно написать CLCDIIVCMCI, и это будет то же самое число. Единственная причина, которая заставляла писцов располагать символы в порядке убывания справа налево, — это удобство считывания числа. Примерно так же, как при игре в бридж — значимость карты всегда остается постоянной, но игроки раскладывают их в порядке убывания справа налево.

В наши дни используют немного измененную систему обозначения. Меньший символ ставят перед большим, когда его надо вычесть из большего. Например, мы привыкли число четыре записывать как IV, а не IIII, а девятьсот как СМ, а не DCCCC. Это усовершенствование древнеримской системы записи чисел было введено уже в Средние века с целью сокращения записи, и древние римляне им не пользовались.

Итак, в римской системе записи значение символа не зависело от его положения, то есть эта система отличается от системы обозначения на счетах, где значение числа зависит от того, в каком ряду оно находится.

Тем не менее и в римской системе обозначения чисел можно производить действия сложения. Например, нам надо сложить MDCCCCLVIIIи MMCCCCLXXII. Запишем новое число, записав знаки обоих чисел вместе. Мы получим:

MMMDCCCCCCCCLLXXVIIIII.

Теперь упростим это выражение:

Пять единиц или IIIII— это V, а два раза по пятьдесят ( LL) — это сто ( С).

Произведем замену и получим: MMMDCCCCCCCCCXXVV.

Но две пятерки ( VV) — это десять, а пять сотен ( ССССС) — это пятьсот ( D). Произведем еще одну замену и получим следующий результат:

MMMDDCCCCXXX.

Но пятьсот и пятьсот ( DD) — это тысяча ( М), проводим последнюю возможную замену и получаем окончательный результат:

ММММССССXXХ,

то есть четыре тысячи четыреста тридцать.

Не сомневайтесь, опытный писец в Древнем Риме мог молниеносно проделать эту операцию. Но есть масса других, крайне необходимых операций с числами, которые очень легко выполнить на счетах и крайне трудно — используя римские цифры.

Именно отсутствие рациональной системы записи чисел остановило развитие математики в Древней Греции, поскольку греки записывали числа не менее громоздким и неудобным способом, чем римляне. Если бы величайший математик древности Архимед владел современной системой записи чисел, он смог бы задолго до Ньютона прийти к идее дифференциального исчисления, а это на восемнадцать веков ускорило бы прогресс науки.