Айзек Азимов - Числа: от арифметики до высшей математики

Когда мы считаем, используя арабские цифры, то первое, что следует сделать, — это запомнить суммы чисел от нуля до девяти. Как мы учимся считать? Сначала запоминаем, что 1 + 1 = 2, 2 + 3 = 5, 4 + 5 = 9, 6 + 7= 13 и так далее. Очень важно также усвоить, что 0 + 0 = 0.

Когда мы считаем на счетах, запоминать ничего не надо. Необходимо только научиться считать от одного до десяти. На этом этапе преимущества расчетов при помощи чисел, записанных на бумаге, еще незаметны. Кажется, что счеты удобнее.

А теперь попробуем сложить два больших числа, например 5894 и 2578. Все, что для этого нужно, — это уметь складывать числа в пределах десяти. Сначала разобьем числа на единицы, десятки, сотни и тысячи, то есть на разряды.

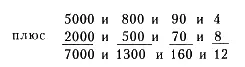
Теперь разобьем число 1300 на 1000 и 300, 160 на 100 и 60, а 12 на 10 и 2. Теперь надо просто прибавить тысячи к тысячам, сотни к сотням, десятки к десяткам. В результате получаем: 8000 и 400 и 70 и 2, то есть 8472.

Упрощенно процесс сложения можно изобразить так:

Упрощение заключается в том, что мы не записываем «нули» и переносим «единицы» в следующий разряд, то есть десятки переносим в колонку десятков и так далее.

Вычитание — это процесс, обратный сложению. Предположим, надо из 531 вычесть 298. Мы также разбиваем числа на разряды:

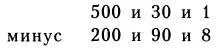
Вначале может показаться, что нам придется вычитать 8 из 1, и 90 из 30. Но это не так, мы ведь можем занять один десяток и одну сотню из следующих разрядов. Перепишем таблицу в новом виде:

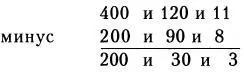
Таким образом, получаем ответ: 233.

Когда мы производим вычитание в столбик, то следуем именно этому принципу, хотя форма записи более упрощенная.

Человек, привыкший считать на счетах, сможет произвести эту операцию гораздо быстрее, чем средний ученик, вычисляющий разность этих двух чисел на бумаге. Однако счеты требуют, кроме всего прочего, наработки чисто механических навыков.

В то же время, когда мы считаем в столбик, мы записываем все этапы, и легко проверить правильность расчетов. Используя счеты, этого сделать нельзя. Метод подсчета в столбик настолько же эффективнее подсчета на счетах, насколько изображение чисел на счетах эффективнее, чем показывать числа на пальцах.

Каждый первоклассник, изучающий арифметику, знает, что сложить можно любые два числа. Он также знает, что к вычитанию это правило не относится.

Можно вычесть 5 из 7 и получить 2. Можно вычесть 7 из 7 и получить 0. А можно ли вычесть 8 из 7?

В Древней Греции на этот вопрос отвечали отрицательно. Как можно произвести действие, в результате которого получается меньше, чем ничего? Ведь «ничего» — это последний предел, дальше идти некуда.

Эта точка зрения торжествовала вплоть до 1500-х годов. А в наши дни кажется совершенно очевидным, что могут существовать числа, меньшие, чем ничего, то есть меньшие ноля.

Предположим, у вас есть семь долларов, а тут к вам подходит ваш приятель и напоминает о вашем долге в восемь долларов. Будучи честным человеком, вы тут же возвращаете ему семь долларов и говорите приятелю, что вернете ему остаток в один доллар, как только получите эту сумму.

Теперь у вас осталось меньше, чем ничего, ведь денег у вас нет, а, напротив, есть долг в один доллар. Другими словами, если из семи вычесть восемь, мы получаем число, на единицу меньшее, чем ноль. Что же тут трудного или непонятного?

Предположим, вы собираетесь дойти до города, который находится в семи километрах к югу от того места, где вы находитесь. Итак, вы идете на юг. Проходите один километр, и вам остается пройти еще шесть, проходите два километра, и вам остается еще пять. Проходите семь километров — и вот вы на месте. До города осталось пройти ноль километров.

Но вы настолько рассеянны (или настолько упрямы), что продолжаете двигаться дальше и проходите еще один километр к югу. Итак, вы прошли восемь километров и оказались на расстоянии в один километр к югу от города. Итак, до города было семь километров, вы прошли восемь. Значит, вы получаете число меньше нуля. Конечно, вы можете сказать, что расстояние начало увеличиваться снова. Но ведь теперь вы двигаетесь в противоположном направлении. Разве это одно и то же?

Для того чтобы прояснить ситуацию, нарисуем вертикальную линию и отметим на ней точкой положение города. Эту точку мы будем считать точкой отсчета или нулем. Теперь нанесем на прямую по несколько равных делений выше и ниже нулевой точки. Пусть каждое деление соответствует одному километру.

Числа выше точки отсчета (то есть к северу от города) будем называть обычными (или положительными), а числа ниже точки отсчета (то есть к югу от города) будем называть числами, меньшими нуля, или отрицательными.

Теперь нам понадобится специальный символ, который поможет различить положительные и отрицательные числа. Обычно для этого используют систему обозначений, основанную на способе, которым можно получить это число. Любое положительное число получается в результате сложения других положительных чисел. Символом сложения является знак «+», поэтому положительные числа обозначаются +1, +2, +3 и так далее. Само название «положительное число» говорит о том, что это число реально существует.

Отрицательные числа получаются как результат вычитания, скажем, при вычитании (2 - 3) мы получаем число на единицу меньше нуля. Его обозначают -1. Таким образом, отрицательные числа обозначают -1, -2, -3, и так далее. [1] Символ (+) перед положительным числом появился где-то в 1500-х годах. В те времена операцию сложения обозначали как &, например «2 плюс 3» записывали как «2&3». В скорописи значок «&» постепенно трансформировался в «φ», а потом в «+». Что же касается происхождения знака «-», то на этот счет существует множество различных теорий, но ни одна из них не кажется достаточно убедительной.

То, что числа, меньшие нуля, получили название отрицательных, не случайно. Даже когда математики освоили операции с числами, меньшими нуля, надо было подчеркнуть, что эти числа не существуют в действительности.

Символ (+) перед положительным числом появился где-то в 1500-х годах. В те времена операцию сложения обозначали как &, например «2 плюс 3» записывали как «2&3». В скорописи значок «&» постепенно трансформировался в «φ», а потом в «+». Что же касается происхождения знака «-», то на этот счет существует множество различных теорий, но ни одна из них не кажется достаточно убедительной.