Айзек Азимов - Числа: от арифметики до высшей математики

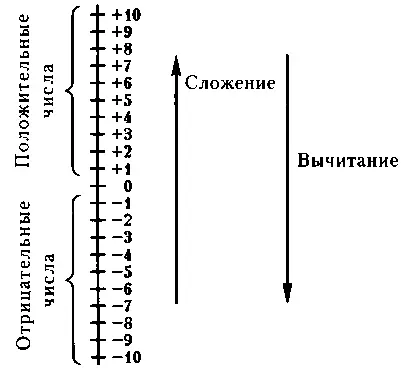
Обратите внимание, ноль не является ни положительным, ни отрицательным числом.

Теперь у нас вертикальная размеченная линия, то есть шкала, и мы можем использовать ее для операций сложения и вычитания. Поскольку положительные числа увеличиваются вверх по шкале, а операции сложения положительных чисел приводят к увеличению чисел, будем считать, что сложение — это движение вверх по шкале. Вычитание — это операция, противоположная сложению, поэтому вычитание — это движение вниз по шкале.

Предположим, надо сложить +2 и +5. Записать это выражение можно следующим образом: (+2) + (+5). Скобки нам понадобились по той причине, что необходимо отделить плюс как знак операции сложения от плюсов, обозначающих положительные числа. Но поскольку мы привыкли к тому, что обычно имеем дело с положительными числами, то часто знаки « + » перед положительными числами просто опускают. Тогда получаем: 2 + 5. Необходимо ставить знаки «+» перед положительными числами только в тех случаях, когда надо привлечь особое внимание к знаку числа.

Теперь отложим на нашей шкале два деления вверх. Это число 2. Прибавим еще 5 делений и остановимся на делении 7, то есть 2 + 5 = 7. Мы можем начать с 5 и прибавить два деления. Мы опять получим 7. Тут я еще раз хочу обратить ваше внимание на тот факт, что от перемены мест слагаемых сумма не меняется.

Теперь займемся вычитанием. Предположим, надо вычесть 2 из 5. От точки 5 на шкале мы откладываем вниз два деления и оказываемся в точке 3. Таким образом, получаем 5-2 = 3.

Теперь нам надо выяснить, как обращаться с отрицательными числами. Можно ли производить с ними такие же действия, как и с положительными числами? Если да, то они окажутся очень полезными, несмотря на то что не являются «настоящими» числами. И действительно, отрицательные числа нашли широчайшее применение не только в науке и инженерной практике, но и в повседневной деятельности. Они применяются, например, в бухгалтерии, где запасы и доходы обозначаются положительными числами, а расходы — отрицательными.

Начнем с простого примера. Определим, чему равно выражение 2 - 5. От точки +2 отложим вниз пять делений, два до нуля и три ниже нуля. Остановимся на точке -3. То есть 2 - 5 = -3. А теперь обратите внимание, что 2-5 совсем не равно 5-2. Если в случае сложения чисел их порядок не имеет значения, то в случае вычитания все обстоит по-другому. Порядок чисел имеет значение.

Теперь перейдем в отрицательную область шкалы. Предположим, надо к -2 прибавить +5. (С этого момента и до конца этой главы мы будем ставить знаки « + » перед положительными числами и заключать в скобки как положительные, так и отрицательные числа, чтобы не путать знаки перед числами со знаками сложения и вычитания.) Теперь нашу задачу можно записать как (-2) + (+5). Чтобы ее решить, от точки -2 вверх поднимемся на пять делений и окажемся на точке +3.

Есть ли в этой задаче какой-то практический смысл? Конечно есть. Предположим, у вас есть долг 2 доллара, а вы заработали 5 долларов. Таким образом, после того, как вы отдадите долг, у вас останется 3 доллара.

Можно также двигаться вниз по отрицательной области шкалы. Предположим, нужно из -2 вычесть 5, или (-2) - (+5). От точки -2 на шкале отложим вниз пять делений и окажемся в точке -7. Какой практический смысл у этой задачи? Предположим, у вас был долг 2 доллара и вам пришлось занять еще 5. Теперь ваш долг равен 7 долларам.

Мы видим, что с отрицательными числами можно проводить такие же операции сложения и вычитания, как и с положительными.

Правда, мы еще освоили не все операции. К отрицательным числам мы прибавляли только положительные числа и вычитали из отрицательных чисел только положительные. А как действовать, если надо складывать отрицательные числа или из отрицательных чисел вычитать отрицательные?

На практике это похоже на операции с долгами. Предположим, с вас списали долг 5 долларов, это означает то же самое, как если бы вы получили 5 долларов. С другой стороны, если я каким-то образом заставлю вас принять ответственность за чей- то долг в 5 долларов, это то же самое, что забрать у вас эти 5 долларов. То есть вычесть -5 — это то же самое, что прибавить +5. А прибавить -5 — это то же самое, что вычесть +5.

Это позволяет нам избавиться от операции вычитания. Действительно, «5 - 2» — это то же самое, что (+5) - (+2) или согласно нашему правилу (+5) + (-2). И в том и в другом случае мы получаем один и тот же результат. От точки +5 на шкале нам нужно спуститься вниз на два деления, и мы получим +3. В случае 5 - 2 это очевидно, ведь вычитание — это движение вниз.

В случае (+5) + (-2) это менее очевидно. Мы прибавляем число, а это означает движение вверх по шкале, но мы прибавляем отрицательное число, то есть совершаем обратное действие, и эти два фактора, взятые вместе, означают, что нам надо двигаться не вверх по шкале, а в обратном направлении, то есть вниз.

Таким образом, мы опять получаем ответ +3.

Почему, собственно, нужно заменять вычитание сложением? Зачем двигаться вверх «в обратном смысле»? Не проще ли просто двигаться вниз? Причина заключается в том, что в случае сложения порядок слагаемых не имеет значения, в то же время в случае вычитания он очень важен.

Мы уже выяснили раньше, что (+5) - (+2) — это совсем не то же самое, что (+2) - (+5). В первом случае ответ +3, а во втором -3. С другой стороны, (-2) + (+5) и (+5) + (-2) в результате дают +3. Таким образом, переходя на сложение и отказываясь от операций вычитания, мы можем избежать случайных ошибок, связанных с перестановкой слагаемых.

Аналогично можно действовать при вычитании отрицательного числа. (+5) - (-2) — это то же самое, что (+5) + (+2). И в том и в другом случае мы получаем ответ +7. Мы начинаем с точки +5 и двигаемся «вниз в обратном направлении», то есть вверх. Точно так же мы бы действовали, решая выражение (+5) + (+2).

Замену вычитания сложением ученики активно используют, когда начинают изучать алгебру, и поэтому эта операция называется «алгебраическим сложением». На самом деле это не совсем справедливо, поскольку такая операция, очевидно, является арифметической, а совсем не алгебраической.

Предположим, мы нарисовали квадрат со стороной в 1 дюйм. Такой квадрат можно назвать квадратным дюймом и использовать его как единицу площади.

Теперь нарисуем квадрат со стороной 2 дюйма, затем разделим каждую сторону пополам и разделим квадрат на четыре части. Каждая часть будет представлять собой 1 квадратный дюйм. Проделаем такую же операцию с квадратом со стороной 3 дюйма, но на этот раз каждую сторону разделим на три части. В результате мы получим 9 квадратов площадью 1 квадратный дюйм каждый.