Бенуа Мандельброт - Фрактальная геометрия природы

Согласно замыслу своего создателя, хаусдорфова размерность сохраняет за собой обязанности обычной размерности и служит показателем степени при определении меры.

Однако с другой стороны, размерность D в высшей степени необычна, — она выражается дробным числом! Мало того, она больше единицы, которая представляет собой «естественную» размерность для кривых (можно строго доказать, что единице равна и их топологическая размерность D T ).

Я предлагаю называть кривые, фрактальная размерность которых превосходит их топологическую размерность 1, фрактальными кривыми. А в качестве краткого резюме для настоящей главы могу предложить следующее утверждение: в географических масштабах береговые линии можно моделировать с помощью фрактальных кривых. Береговые линии по своей структуре фрактальны.

Рис. 55. ОБЕЗЬЯНЬЕ ДЕРЕВО

На данном этапе этот небольшой рисунок следует рассматривать просто как декоративный элемент, он всего лишь заполняет пустое место.

Однако после прочтения главы 14 читатель сможет обнаружить здесь подсказку для распутывания «архитектурной» загадки на рис. 210. Более серьезную подсказку дает нижеприведенный генератор:

Если у математика возникает необходимость «приручить» какую-нибудь особенно нерегулярную кривую, он может воспользоваться следующей стандартной процедурой: выбирается некое значение ε , и вокруг каждой точки кривой строится круг радиуса ε . Эта процедура, восходящая, по меньшей мере, к Герману Минковскому, а то и к самому Георгу Кантору, несколько грубовата, но зато весьма эффективна. (Что касается термина сосиска, то его происхождение, согласно непроверенным слухам, как-то связано с применением Норбертом Винером данной процедуры к броуновским кривым.)

На помещенных здесь иллюстрациях вышеописанное сглаживание применяется не к реальным берегам, а к одной теоретической кривой, которую мы построим несколько позже (см. рис. 79) путем постоянного добавления все более мелких деталей. Сравнивая изображенный справа кусок сосиски с правым концом сосиски, помещенной вверху, мы видим, что критический этап в построении кривой наступает, когда кривая начинает включать в себя детали меньшего, чем ε , размера. На более поздних этапах сосиска существенно не изменяется.

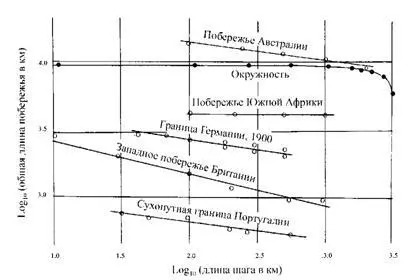
Рис. 57. ЭМПИРИЧЕСКИЕ ДАННЫЕ РИЧАРДСОНА ОТНОСИТЕЛЬНО СКОРОСТИ РОСТА ДЛИН БЕРЕГОВЫХ ЛИНИЙ

На этом рисунке приведены экспериментальные результаты измерения длины кривой, произведенные на различных кривых с использованием равносторонних многоугольников с уменьшающейся длиной стороны ε . Как и ожидалось, в случае окружности измерения с возрастающей точностью дают величину, которая очень быстро стабилизируется около вполне определенного значения.

В случае береговых линий приближенные значения длины, напротив, не стабилизируются вовсе. По мере того, как длина шага ε стремится к нулю, аппроксимативные значения длины, отложенные в дважды логарифмической системе координат, образуют прямую с отрицательным наклоном. Так же обстоит дело и с сухопутными границами между странами. Наведенные Ричардсоном в различных энциклопедиях справки вскрыли значительные различия в определении длины общей границы картографами соответствующих стран: например, длина границы между Испанией и Португалией составляет 987 км с точки зрения испанцев и 1214 км с точки зрения португальцев; аналогичным образом пострадала и граница между Нидерландами и Бельгией (380 и 449 км). Так как угловой коэффициент соответствующих прямых равен -0,25, двадцатипроцентная разница между результатами измерений означает двукратную разницу между принятыми для этих измерений значениями ε — не такое уж невероятное предположение.

Ричардсон не дал никакой теоретической интерпретации различному наклону своих прямых. Мы же с вами намерены интерпретировать береговые линии как приближения к фрактальным кривым и рассматривать угловые коэффициенты соответствующих им прямых как приближенные значения разности 1−D , где D — фрактальная размерность.

Для более полного понимания моей интерпретации ричардсонова D как фрактальной размерности перейдем от природных феноменов, над которыми мы не имеем никакой власти, к полностью подвластным нашей воле геометрическим конструкциям.

До сих пор мы больше уделяли внимание геометрической сложности береговых линий; настало время упомянуть и о том, что их структура в значительной степени упорядочена.

Хотя выполненные в разных масштабах карты и различаются в конкретных деталях, более общие их особенности остаются неизменными. В грубом приближении крупные детали береговых линий геометрически идентичны мелким, разница только в масштабе.

Такую форму можно сравнить с узором, который рисует на небе какой-нибудь многоступенчатый фейерверк: на каждом этапе его сгорания в общую картину добавляются новые, все более мелкие детали, идентичные по форме результату исходного взрыва. Однако из упоминавшихся выше трудов Льюиса Ричардсона, посвященных турбулентности, мы можем позаимствовать более подходящее сравнение и назвать порождающий такие структуры механизм каскадом.

Если каждая из частей некоторой формы геометрически подобна целому, то и форма, и порождающий ее каскад называются самоподобными. В настоящей главе мы займемся исследованием самоподобия, используя для этого самые что ни на есть правильные фигуры.

Наиболее полную противоположность самоподобным формам представляют собой кривые, которые имеют либо только один масштаб (например, окружность), либо два четко разделенных масштаба (например, окружность, украшенная «гребнем» из множества меньших полуокружностей). Такие формы мы можем охарактеризовать как немасштабируемые.

Если мы хотим получить кривую, содержащую бесконечное число масштабов длины, то надежнее всего будет ввести их туда собственноручно, один за другим. Правильный треугольник с длиной стороны, равной 1, имеет один масштаб, правильные треугольники с длиной стороны, равной 1/3, также имеют один масштаб, только меньший — уменьшая длину стороны далее по правилу (1/3) k , мы будем получать треугольники все меньшего масштаба. Нагромоздив затем все эти треугольники друг на друга (как показано на рис. 70), получим форму, содержащую все масштабы, меньшие 1.