Бенуа Мандельброт - Фрактальная геометрия природы

Рис. 79. ПРОЧИЕ ОСТРОВА И ОЗЕРА КОХА (РАЗМЕРНОСТИ БЕРЕГОВЫХ ЛИНИЙ ОТ 1 ДО D= ln3 / ln√5 ~1,3652 )

В данной последовательности фрактальных кривых инициатором выступает правильный многоугольник с числом сторон M генератор таков, что N=3 , а углы между его первым и вторым и вторым и третьим отрезками совпадают и равны θ=2π/M . На рис. 75 и 76 M=6 (здесь этой фигуры нет), а кривая с M=3 обсуждается в пояснении к рис. 109. На данном рисунке изображены поздние стадии построения терагонов для значений M = 4, 8, 16 и 32 в виде вложенных друг в друга озер и островов. Например, значению M=4 соответствует следующий генератор:

Штриховка внутри центрального острова ( M=4 ) описана в пояснении к рис. 109 и 110.

Если параметр M уходит в бесконечность, соответствующая кривая стремится приобрести форму окружности. Если же M уменьшается, то наши фигуры начинают «съеживаться», сначала постепенно, затем — резкими скачками. Когда M достигает 3, в соответствующей кривой появляются самопересечения. Этот случай мы обсудим позже (см. рис. 109 и 110).

Критическая размерность. Когда в качестве инициатора выбирается отрезок [0, 1], угол θ может принимать любые значения от 180 градусов до 60 градусов. Существует, однако, некий критический угол θ kp — такой, что береговая линия не имеет самопересечений в том и только в том случае, если θ>θ kp . Соответствующая размерность D kp называется критической размерностью для самопересечений. Угол θ kp близок к 60 градусам.

Обобщение. Построения, изображенные на рис. 75-88, допускают следующее несложное обобщение. Назовем приведенные на рисунке генераторы прямыми (S) и определим обратный генератор (F) как зеркальное отражение прямого генератора относительно линии y=0 . На каждом отдельном этапе построения будем использовать один генератор, однако для различных этапов можно выбирать различные генераторы. Кривые на указанных (и некоторых последующих) рисунках построены с помощью S-генераторов, но и другие бесконечные последовательности S- и F-генераторов дают очень похожие результаты.

< При чередовании F- и S-генераторов локсодромические точки переходят в гиперболические, как в оригинальной кривой Коха. ►

На рис. 79-85 показано несколько фигур Коха, инициатором которых является квадрат (отсюда и название квадратичные). Одним из преимуществ таких построений является то, что с ними можно экспериментировать даже на слабых графических системах. < Еще одно преимущество — квадратичные фрактальные кривые ведут непосредственно к оригинальной кривой Пеано, описанной в пояснении к рис. 95. ►

Рис. 81. Инициатором здесь служит квадрат, а генератор выглядит следующим образом:

Как и на рис. 75-79, на каждом этапе построения общая площадь острова остается неизменной. На рис. 81 вверху приведены два первых этапа построения крупным планом и два последующих в более мелком масштабе.

Результат последнего этапа, еще более увеличенный, демонстрирует мельчайшие детали в виде очень тонких, едва видимых выступов, которых вы, конечно же, не увидели бы, не обладай наша графическая система такой превосходной разрешающей способностью.

Как в терагонах, так и в предельной кривой отсутствует какое бы то ни было самоперекрытие, самопересечение или самокасание. Это утверждение остается в силе и для последующих построений (вплоть до рис. 85).

< Не следует забывать о том, что фракталы на рис. 81-85 представляют береговые линии; суша и море здесь — это удобные фигуры, обладающие положительными и конечными площадями. На с. 209 упоминается случай, в котором только «море», будучи объединением простых трем, имеет вполне определенную площадь, в то время как суша не имеет ни единой внутренней точки. ►

Тайлинг и пертайлинг.Этот остров можно разбить на 16 меньших островков ( r=1/4 ). Каждый представляет собой остров Коха, построенный на одном из 16 квадратов, образующих первый этап построения.

< В главах 25 и 29 показано, что размерность D=3/2 характерна также для многих броуновских функций. Следовательно, это значение легко можно получить с помощью случайных кривых и поверхностей. ►

Рис. 81. КВАДРАТИЧНЫЙ ОСТРОВ КОХА (РАЗМЕРНОСТЬ БЕРЕГОВОЙ ЛИНИИ D=3/2=1,5000 )

В качестве инициатора снова возьмем квадрат, а генератором будет следующая ломаная:

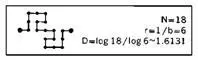
То, что береговая линия квадратичных островов Коха, представленных в данной подборке иллюстраций, в очень значительной степени зависит от D , весьма показательно. В то же время, поскольку их общим инициатором является квадрат, внешняя форма этих островов остается приблизительно одинаковой. Если инициатором выступает какой-либо другой правильный M -угольник ( M>4 ), то можно наблюдать, как по мере увеличения M внешняя форма становится все более гладкой. Об истинной зависимости между внешней формой и значением D мы узнаем не раньше, чем в главе 28, в которой рассматриваются случайные береговые линии, эффективно определяющие как генератор, так и инициатор.

< Максимальность.Свой вклад в сходство внешних форм вносит тот факт, что изображенные на рис. 79-85 квадратичные кривые Коха обладают весьма интересным свойством максимальности. Расположим все генераторы Коха, порождающие кривые без самопересечений, на квадратной решетке, образованной прямыми, параллельными и перпендикулярными отрезку [0, 1]. Допустим также, что все эти генераторы можно использовать с любыми инициаторами на нашей квадратной решетке. Определим как максимальные те генераторы, которые характеризуются наибольшим значением N и, как следствие, D . Нетрудно заметить, что N max =b 2 /2 при четных b и N max =(b 2 +1)/2 при нечетных b .

При увеличении b возрастает как максимальное значение N , так и число альтернативных максимальных многоугольников. Таким образом, на предельную кривую Коха все большее влияние оказывает исходный генератор. Кроме того, кривая выглядит все более изощренной, поскольку стремление достичь максимальной размерности, избежав при этом самопересечения, налагает определенные требования, которые лишь ужесточаются с ростом D . Этот процесс достигает кульминации в следующей главе, вместе с пределом Пеано D=2 .