Бенуа Мандельброт - Фрактальная геометрия природы

< Строго говоря, масштабно-инвариантные фракталы были призваны представлять только те кластеры, которые не усечены границей исходной решетки. Это исключает из рассмотрения сам перколяционный кластер. (Термин кластер обладает чудесным даром создавать путаницу, вы не находите?) Для объяснения возникающего осложнения представим себе чрезвычайно большую решетку, выберем на ней какой-нибудь кластер и квадрат меньшего размера, наложенный на этот кластер. По определению, пресечение кластера и квадрата включает в себя меньший перколяционный кластер, однако оно же включает в себя и «остаток», который соединяется с меньшим перколяционным кластером посредством связей, находящихся вне квадрата. Заметим, что пренебрежение этим остатком смещает вниз оценку D c . ►

Неслучайные фрактальные модели — очень приближенные, но конкретные.Для того, чтобы утверждение о фрактальной природе какого-либо естественного феномена было обоснованным, его следует сопроводить описанием конкретного фрактального множества, которое могло бы послужить моделью этого явления в первом приближении или хотя бы дать нам возможность представить его перед мысленным взором. Моя модель береговых линий, основанная на кривых Коха, или модель галактических скоплений Фурнье показывают, что такое приближенное неслучайное представление может оказаться весьма полезным. Я полагаю также, что рекурсивно построенные контактные кластеры (подобные тем, что рассматриваются в этой главе) могут снабдить нас полезными фрактальными моделями слабо изученного естественного феномена, который обычно моделируется кластерами Бернулли.

Однако сами кластеры Бернулли полностью изучены (по крайней мере, принципиально), и следовательно, их моделирование с помощью явных рекурсивных фракталов представляет собой несколько иную задачу. Рассмотренные мною коховы контактные кластеры для этого случая не годятся из-за асимметрии между виниловыми и медными стержнями, которая сохраняется даже при равных количествах стержней обоих видов. Далее на очереди заузленные кластеры Пеано. Возьмем терагон на некотором отдаленном этапе построения и покроем ячейки, расположенные слева от кривой, медью, а остальные — винилом. Результат представляет собой форму перколяции относительно ячеек решетки (или их центров, называемых узлами). Задача становится симметричной. Однако она отлична от задачи Бернулли, так как получаемая конфигурация медных и виниловых ячеек очень отличается от той, какой она могла бы быть при независимом их распределении: например, в бернуллиевой решетке девять ячеек, образующих суперквадрат, могут целиком состоять из меди или винила, тогда как в случае заузленной кривой Пеано это невозможно. (С другой стороны, обе модели позволяют группам из четырех ячеек, образующих суперквадрат, принимать любые возможные конфигурации.) Эта разница имеет далеко идущие последствия: например, в задаче о бернуллиевой перколяции по узлам с p=1/2 не перколируют ни медь, ни винил, тогда как в случае заузленных кластеров Пеано перколируют и медь, и винил (учитывая, что p=1/2 — критическая вероятность).

Перечень вариантов бернуллиевой перколяции по связям уже довольно обширен и может быть с легкостью продлен. Я же успел рассмотреть множество вариантов рекурсивно построенных фрактальных контактных кластеров. Детальное сравнение этих двух перечней, к сожалению, заняло бы слишком много места, и потому я не стану приводить его здесь.

Позвольте мне ограничиться весьма расплывчатым выводом о том, что фрактальная сущность задачи о бернуллиевой перколяции в значительной степени иллюстрируется неслучайными заполняющими пространство σ -кластерами, определенными ранее в этой главе. Основная слабость данной модели заключается в том, что за пределами уже сказанного она остается совершенно неопределенной. Ее можно подогнать к любой степени иррегулярности и фрагментации. На предмет топологии см. главу 14.

Модель критических кластеров.Рассмотрим, в частности, критические кластеры, определяемые как кластеры при p=p крит. Для их представления экстраполируем рекурсивный σ -кластер, как показано ранее в этой главе. Затем, остановив интерполяцию, усечем его таким образом, чтобы положительный внутренний порог оказался равен размеру ячейки в исходной решетке.

Модели некритических кластеров.Для того, чтобы распространить эту геометрическую картину на некритические кластеры, т. е. на кластеры при p≠p крит, нам необходимы фракталы с положительным внутренним и конечным внешним порогами. Аналитические рассуждения показывают, что протяженность наибольшего медного кластера составляет величину порядка ξ при p

крити уходит в бесконечность при p>p крит. Оба варианта легко осуществимы. Можно, например, начать с того же генератора, что и в предыдущем подразделе, однако вместо естественной его экстраполяции, подставим в качестве инициатора одну из следующих фигур:

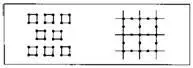
Докритические кластеры.Инициатор на рисунке слева (построенный с таким расчетом, чтобы p

крит) составлен из квадратов с длиной стороны ξ/2 . Применяя выбранный генератор к левым сторонам квадратов, будем помещать его внутри квадратов, во всех же остальных случаях — снаружи. Квадрат инициатора превратится при этом в нетипичный кластер протяженности ξ , окруженный множеством типичных кластеров протяженности <���ξ .

Сверхкритические кластеры.Инициатор на рисунке справа (построенный так, чтобы p>p крит) составлен из тех линий исходной квадратной решетки, координаты которых ( x или y ) являются четными целыми числами. Из каждого узла (координаты которого являются четными целыми числами) исходят по четыре связи; выбранный генератор всегда помещается слева. В особом случае, когда берег-генератор не содержит ни петель, ни свободных концов, получающаяся картинка представляет собой дерандомизированный и систематизированный вариант грубой модели кластеров, основанной исключительно на «узлах и связях».

Заметим, что фрактально-геометрическое представление выводит некритические кластеры из критических, в то время как физики предпочитают рассматривать критические кластеры как предельный случай некритических кластеров при ξ→∞ .

Значение D c непосредственно выводится либо из показателя D/D c =E/D c в формуле для Nr(M>μ) , либо из показателя Q=2D c −D=2D c −E в формуле для . Введя греческие буквы τ , σ и η в обычном для данного контекста значении, получим E/D c=τ−1 и 2D c −E=2−η . Отсюда