Бенуа Мандельброт - Фрактальная геометрия природы

Применение вышеупомянутого принципа к кластеризации галактик ставит перед исследователем весьма непростые задачи. Вселенная Фурнье (см. главу 9), разумеется, донельзя неоднородна, но, может быть, есть еще надежда на то, что нам удастся рандомизировать эту модель с тем, чтобы привести ее в соответствие с однородным космографическим принципом. Однако для сохранения в неприкосновенности духа модели необходимо, чтобы при рандомизации не пострадало то ее свойство, согласно которому приблизительная плотность M(R)R −3 в сфере радиуса R стремится к 0, когда R→∞ . К сожалению, это свойство и однородный статистический космографический принцип суть вещи несовместимые.

Возникает искушение придать большее значение общему принципу, нежели всего лишь данным, и сделать вывод, что иерархическая кластеризация должна по достижении некоторого конечного верхнего порога прекратиться, т.е. все флуктуации являются локальными по своей протяженности, а общая плотность материи все же отлична от нуля.

Для осуществления этой идеи можно, например, взять бесконечное множество вселенных Фурнье и разбросать их повсюду статистически однородным образом. Еще один вариант, предложенный Р. М. Сонейрой, обсуждается в книге [467].

Я все же полагаю, что однородный статистический космографический принцип, пожалуй, выходит за рамки разумного и желательного и что его следует заменить еще более ослабленной формой (назовем ее условной), которая относится не ко всем наблюдателям, а только к материальным. Астрономы, должно быть, сочли бы такой принцип вполне приемлемым и давно взяли бы его на вооружение, заподозри они, что от него может быть хоть какая-то реальная польза. А польза есть: условная форма не содержит никаких допущений относительно глобальной плотности и признает соотношение M(R)∝R D−3 .

Попробую теперь выразить мысли в менее напористой манере. Известно, что примирить усиленный космографический принцип с тем обстоятельством, что действительное распределение галактик чрезвычайно далеко от однородного, - задача очень сложная, если не вовсе невыполнимая. С одной стороны, если глобальная плотность δ материи во Вселенной стремится к нулю, то усиленный космографический принцип, должно быть, неверен. С другой стороны, если величина δ мала, но отлична от нуля, то усиленный космографический принцип выполняется асимптотически, хотя в интересующих нас масштабах от него нет никакой пользы. Вы, возможно, захотите держать его про запас, если вас это успокаивает. Возможно также, что вы предпочтете отбросить его совсем во избежание потенциальных недоразумений. Наконец, вы можете удовлетвориться заменой его на другой принцип, который имеет смысл во всех масштабах и независим от того, равна нулю или положительна плотность δ . Последний подход предполагает разбиение усиленного космографического принципа на две части.

Условное распределение.В тех случаях, когда начало системы отсчета само является материальной точкой, вероятностное распределение масс называется условным.

Основное космографическое допущение.Условное распределение масс одинаково для всех удовлетворяющих условию систем отсчета. В частности, масса M(R) , заключенная внутри шара радиуса R , является случайной величиной, независимой от системы отсчета.

Формулировка условного космографического принципа звучит совершенно одинаково как для случая δ>0 , так и для случая δ=0 . Это принято с эстетической стороны и имеет преимущества со стороны философской, поскольку согласуется с духом современной физики. Разделяя усиленный космографический принцип на две части, мы получаем возможность выдвинуть на первый план утверждение, которое справедливо для всего, что мы можем наблюдать, и не придавать излишнего значения утверждению, которое является не более чем актом веры, - в лучшем случае, рабочей гипотезой.

Вспомогательное космографическое допущение.Величины

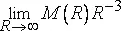и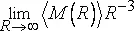

существуют, почти наверняка равны между собой, положительны и конечны.

Статистические законы распределения материи можно формулировать различными способами. Можно воспользоваться при этом абсолютным распределением вероятностей относительно системы отсчета, центром которой является материальная точка. В том случае, когда вышеупомянутое вспомогательное допущение подтверждается, условное распределение вероятностей выводится из абсолютного с помощью самого обыкновенного правила Байеса. А абсолютную вероятность можно вывести из условной вероятности, найдя среднее из значений последней относительно начал отсчета, однородно распределенных в пространстве.

Начала отсчета, однородно распределенные по всему пространству, обладают, в общей сложности, бесконечной массой. Неусловное распределение можно переформировать – с тем, чтобы свести его к единице – тогда и только тогда, когда глобальная плотность положительна. См. [352].

Представим теперь обратную ситуацию – такую, в которой вспомогательное допущение ложно, а точнее, в которой предел 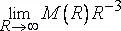обращается в нуль. В этом случае абсолютное распределение вероятностей указывает лишь на то, что некий случайно выбранный шар конечного радиуса R почти наверняка окажется пустым. А значит тот, кто сидит на выбранной в пространстве случайным образом точке и глазеет по сторонам, почти наверняка ничего не увидит. Однако вероятностное распределение масс интересно человеческим существам лишь в той степени, в какой оно объясняет положение дел в реальной Вселенной, где как известно, масса в нуль не обращается, по крайней мере, в окрестности места обитания этих самых существ. После того, как событие произошло, абсолютная вероятность именно этого события представляет весьма ограниченный интерес.

Тот факт, что неусловное распределение автоматически пренебрегает подобными случаями, говорит о вопиющей его неадекватности при δ=0 . Оно не только не совместно с массой, содержащейся в любом фрактале с размерностью D<3 , но и не сообщает нам абсолютно ничего, кроме того, что δ=0 .