Бенуа Мандельброт - Фрактальная геометрия природы

Построение простейшей случайной пыли, способной усовершенствовать канторову модель ошибок при передаче (см. главу 8), начинается с простейшей формы канторова створаживания: с решетки интервалов с базой b и некоторого целого числа N . Однако вместо одного конкретного генератора нам предлагается список всех возможных канторовых генераторов, т.е. всех различных рядов, состоящих из N заполненныхи b−N пустыхпромежутков. На каждом этапе построения случайным образом и с одинаковой вероятностью выбирается один из этих генераторов.

Любая принадлежащая творогу точка P определяется последовательностью вложенных «предтворожных» интервалов с длинами R k =b −k . Если общая исходная масса рана 1, то каждый предтворог содержит одинаковую массу R k D . Масса, содержащаяся в интервале длины 2R k с центром в точке P , равна произведению R k D на некоторую случайную величину, лежащую в интервале от 1 до 2 и не зависящую от k .

Заметим, что размерность D ограничена последовательностью ln (b−1)/ ln b, ln (b−2)/ ln b,... . Это ограничение часто причиняет неудобства. Что более важно, вышеприведенное определение створаживания сложно реализуется в компьютерной программе и вообще плохо поддается аналитическим манипуляциям. Так как главное достоинство модели створаживания заключается в ее простоте, более предпочтительным, очевидно, окажется альтернативное определение, которое мы дадим в последующих разделах. Во избежание путаницы будем называть определение, приведенное в этом разделе, ограниченным (в [378] я предлагал иной термин: микроканоническое определение).

Более удобное определение створаживания (предложенное в [378], где я называю его каноническим) можно получить с помощью последовательности случайных двоичных выборов, каждый из которых определяется простым броском монеты. Бросок монеты на первом этапе решает последующую судьбу каждого из b подынтервалов. Если выпадает орел (событие с вероятностью p<1 ), то данный подынтервал «выживает» как часть предтворога; в противном случае мы с ним больше не встретимся. Изолированные точки, остающиеся между «мертвыми» подынтервалами любой длины, после каждого этапа стираются. Здесь, конечно, от них вреда немного, однако их плоскостные или пространственные аналоги (изолированные линии и т.д.) порождают в множестве ложную связность. Ожидаемое количество выживших подынтервалов равно =pb=p/r . Далее процесс возобновляется, причем каждый подынтервал обрабатывается независимо от других.

Формализм процесса рождения.Если назвать подынтервалы «детьми», а весь каскад – «семьей», то сразу станет ясно, что распределение количества детей определяется известным процессом рождения и гибели (см. [196]).

Фундаментальным следствием этого наблюдения является существование для величины критического значения: этот факт был открыт в 1845 году Иренеем Бьянеме (см. [212]) и вполне заслуженно называется эффектом Бьянеме.

Значение =1 является критическим в том смысле, что количество N(m) наличествующих в m - м поколении отпрысков ставит нас перед очень простой альтернативой. Если ≤1 , то семейство почти наверняка вымрет, и в настоящей интерпретации это означает, что каскад даст, в конце концов, пустое множество. Если же >1 , то генеалогическая линия каждого творога имеет ненулевую вероятность продолжиться на бесконечное число поколений. В этом случае случайное створаживание дает в пределе случайную линейную пыль.

Смысл размерности подобия.Так как отношение ln N(m)/ ln (1/r) здесь изменяется случайным образом, понятие размерности подобия требует переосмысления. Из почти истинного соотношения

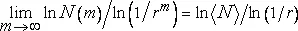
можно предположить, что обобщенная размерность подобия выглядит следующим образом:

D *=ln/ln(1/r)=E−lnp/ln(1/r) .

При таком определении D * условие существования непустого предельного множества >1 принимает весьма логичный вид: D * >0 . Если D * >0 , то D=D * . Если же мы формально применим эту формулу к случаю ≤1 , то получим D≤0 , однако фактически размерность D пустого множества всегда равна 0.

Построим последовательность случайных творогов с уменьшающейся размерностью D , каждый из которых вложен в предыдущий.

Предварительный этап не зависит от величины D и заключается в присвоении каждому вихрю (неважно какого порядка) некоторого случайного числа U из интервала от 0 до 1. Из главы 21 нам известно, что все эти числа, взятые в совокупности, эквивалентны одному – единственному числу, которое служит мерой вклада случайности в данный процесс. Далее выбираем значение D и определяем из последней записанной нами формулы порог вероятности p . Наконец, происходит собственно створаживание посредством, если можно так выразиться процесса «фрактальной децимации». При U>p вихрь «умирает», переходя в простоквашу и унося с собой все свои субвихри. Если же U≤p , то вихрь можно считать выжившим и готовым к дальнейшему створаживанию.

Этот метод позволяет представлять все характеристики творога, простокваши и всех остальных интересующих нас множеств в виде функций от непрерывно изменяющейся размерности. Достаточно зафиксировать случайные числа U , уменьшая при этом значение p от 1 до 0, и мы получим размерность D , уменьшающуюся от 3 до 0.

Пусть даны твороги Q 1 и Q 2 , соответствующие вероятностям p 1 и P 2

1 и имеющие размерности D 1 и D 2 1 . Тогда преобразование Q 1 в Q 2 ⊂Q 1 можно назвать «относительной фрактальной децимацией» и охарактеризовать относительной вероятностью p 2 /p 1 и относительной размерностью D 2 −D 1 . Для того, чтобы произвести относительную децимацию вручную, следует разыскать вихри со стороной 1/b , принадлежащие множеству Q 1 , и определить их дальнейшую жизнь вероятностью p 2 /p 1 . Затем поступаем аналогичным образом с выжившими вихрями (длина стороны 1/b 2 ) и т.д. Относительные вероятности в получающемся путем последовательных децимаций ряду Q 1 ,Q 2 ,...,Q g перемножаются, а относительные размерности складываются ... до тех пор, пока значение суммы не становится отрицательным, а множество Q - пустым.