Бенуа Мандельброт - Фрактальная геометрия природы

Сыр.Образ, стоящий за термином створаживание (равно как и за термином сыворотка, обозначающим дополнение творожного множества), не следует, разумеется, воспринимать буквально, однако известно, что образование реального сыра может быть вызвано биохимической нестабильностью – точно так же, как створаживание Новикова – Стюарта происходит, согласно предположению, вследствие нестабильности гидродинамической. Как бы то ни было, неопровержимых данных в пользу того, что какой-нибудь съедобный сыр может оказаться, ко всему прочему, еще и фрактальным, у меня нет.

Известно, что в трехмерном пространстве стандартные фигуры с размерностью D<3 (точки, линии и поверхности) имеют нулевой объем. Это верно и для случайного творога.

Площадь предтворогов также ведет себя довольно просто. При D>2 она стремится к бесконечности, а при D<2 - к нулю. При D=2 створаживание практически не изменяет величину площади.

Аналогичным образом, по мере того, как m→∞ , суммарная длина краев предтворогов стремится к бесконечности при D>1 и к нулю при D<1 .

Эти свойства можно считать еще одним подтверждением того, что творог с фрактальной размерностью, заключенной в интервале 2 , представляет собой нечто среднее между обычной поверхностью и объемной фигурой.

Доказательства.Самым простым оказывается доказательство для случая ограниченного створаживания. Объем m - го предтворога равен L 3r 3mN m=L 3(r 3−D) m , и величина эта стремится к нулю по мере уменьшения внутреннего масштаба η=r m . Что касается площади, то случай D<2 устанавливается по верхнему пределу. Площадь предтворога m - го порядка не может превышать суммы площадей соответствующих вихрей, так как упомянутая сумма включает в себя те стороны субвихрей, которые, являясь общими для соседних творогов, нейтрализуют одна другую. Поскольку площадь каждого вихря m - го порядка составляет 6L 2 r 2m , их общая площадь не может превышать 6L 2r 2mN m=6L(r 2−D) m . При D<2 верхний предел стремится к нулю по мере того, как m→∞ , что доказывает наше утверждение. В случае D>2 мы можем получить нижний предел, отметив, что объединение вихрей m - го порядка, содержащихся в предтвороге m - го порядка, включает в себя, по крайней мере, один квадрат с длиной стороны r m и площадью r 2m , каковой квадрат достается нам в наследство от предтворога (m−1) - го порядка и никак не может быть меньше, чем L 2r 2mN m−1=(L 2/N)(r 2−D) m , а эта величина стремится к бесконечности вместе с m . Наконец, при D=2 оба предела оказываются конечными и положительными.

Наша следующая тема уже неоднократно упоминалась ранее. И вот теперь мы созрели для того, чтобы рассмотреть ее в полном и явном виде на примере одного особого случая.

Для начала припомним следующее стандартное свойство евклидовой геометрии плоскости: если размерность D некоторой фигуры удовлетворяет условию D≥1 , то сечение этой фигуры прямой (если оно не пусто) «обычно» имеет размерность D−1 . Например, непустое линейное сечение квадрата (D=2) представляет собой отрезок с размерностью 1=2−1 . А линейное сечение прямой (D=1) - это точка (размерность 0=1−1 ), за исключением случая, когда обе прямые совпадают.

Стандартные геометрические правила, определяющие поведение размерности при пересечении, можно свести к следующему, более общему виду: если сумма коразмерностей C=E−D меньше E , то эта сумма является коразмерностью типичного пересечения; в противном случае пересечение, как правило, оказывается пустым. (Я приглашаю читателя самостоятельно проверить справедливость данного утверждения для различных пространственных конфигураций плоскостей и прямых.)

Упомянутое правило, к счастью, распространяется и на фрактальные размерности. Благодаря этому обстоятельству многие относящиеся к фракталам рассуждения становятся гораздо более простыми, чем можно было опасаться. Не следует, однако, забывать и о многочисленных исключениях из правила. Так, в частности, в главе 14 мы наблюдали, что при пересечении неслучайного фрактала J особым образом расположенной прямой или плоскостью далеко не всегда можно вывести размерность получающегося сечения из размерности фрактала J . Случайные фракталы в этом смысле заметно проще.

Для доказательства применимости этого фундаментального правила к фрактальному творогу рассмотрим следы (квадраты и интервалы), оставляемые вихрями и субвихрями каскада створаживания на поверхности либо на краю исходного вихря со стороной L . На каждом этапе каскада каждый участок предтворога замещается некоторым количеством меньших участков, причем количество это определяется процессом рождения и гибели. Обозначим количество «отпрысков» m - го поколения, расположенных вдоль края исходного вихря, через N 1 (m) . Классические выводы, уже использованные ранее в этой главе, показывают, что величина N 1 (m) не оставляет нам богатого выбора. Если 1>=Nr 2≤1 (т.е. D≤2 ), то можно быть почти уверенным, что семейство, в конце концов, вымирает, иными словами край вихря становится пустым, а размерность его, как следствие, равной нулю. Если же 1>>1 (т.е. D>2 ), то генеалогическая линия каждого края имеет, напротив, ненулевую вероятность продолжиться на бесконечное число поколений. Размерность подобия в этом случае равна D−2 согласно следующему почти всегда верному соотношению:

.

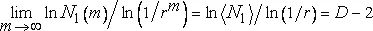К двумерным следам вихрей применимы те же рассуждения, только нужно заменить величину N 1 на некоторую случайную величину N 2 - такую, что 2>=Nr . Если 2>≤1 (т.е. D≤1 ), то поверхность каждого вихря становится, в конце концов, пустой. Если же 2>>1 (т.е. D>1 ), то размерность подобия равна D−1 согласно следующему почти верному соотношению:

.

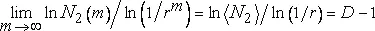При ограниченном створаживании результаты остаются такими же.