Бенуа Мандельброт - Фрактальная геометрия природы
- Название:Фрактальная геометрия природы
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:2002
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Бенуа Мандельброт - Фрактальная геометрия природы краткое содержание
Для студентов и аспирантов, физиков и математиков, инженеров и специалистов.
Фрактальная геометрия природы - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
В этом свете факт наличия весьма серьезных ограничений, налагаемых геометрией плоскости на построение сквиг – кривых (в результате чего сквиг - кривые получаются более предсказуемыми и менее разнообразными), выглядит достоинством.
РАЗМЕРНОСТЬ D~4,3
Следует обратить самое пристальное внимание на размерность сквиг – кривых D~4,3 . То, что мы еще не раз встретимся с этим значением – в главе 25 (рис. 341) и в главе 36 – вряд ли можно объяснить простым совпадением; не исключено, что он приведет нас к более глубокому проникновению в основы геометрической структуры плоскости.
ВЕТВЯЩИЕСЯ СКВИГ - КРИВЫЕ
Вернемся к построению речного русла. Вот мы заменили треугольный интервал долины участком поддолины, состоящим из одного или трех подтреугольников; представьте теперь, что оставшиеся три (или один) подтреугольника вдруг решают отвести от основного русла собственную поддолину. Построение нового русла полностью определяется уже известным процессом. Точки, в которых подреки пересекают границы между треугольниками, выбираются с помощью той же системы, что используется в главной реке. В пределе конструкция сходится к древовидной кривой, которая заполняет треугольник случайным образом, как можно видеть на рисунке:
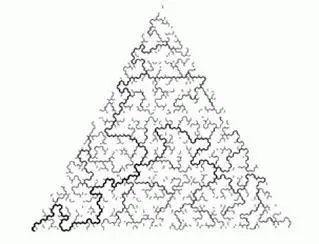
ОЧЕНЬ КРАТКО ЕЩЕ О ДВУХ ПРЕЦЕДЕНТАХ
Тот факт, что столь грубая модель, как мои линейные сквиг – кривые, может дать результат, вполне сносно – хоть и приблизительно – согласующийся с наблюдаемой размерностью реальных речных русел и бассейнов, представляется мне весьма интересным и даже многозначительным.
С помощью этих кривых можно также найти размерность общепринятой модели для сильно разбавленных растворов линейных полимеров – случайного блуждания без самопересечений (СББС) на решетке (см. главу 36).
Лучшая (чем в случае СББС) приспособленность сквиг – кривых к ограничениям, налагаемым геометрией плоскости, объясняется, очевидно, интерполяционным характером их построения.
СКВИГ–ПОВЕРХНОСТИ
Сквиг – поверхности строятся на кубе, разделенном на b 3 подкубов; я определил соответствующие «освобождающие» процедуры, которые однозначно определяют получаемую в результате фигуру – нечто вроде скомканного шерстяного шарфа постоянной и в то же время уменьшающейся толщины. К сожалению, не представляется возможным привести здесь алгоритм построения, из-за его чрезмерной громоздкости.
Во многих случаях кривую Коха с заранее заданной размерностью D и без самопересечений можно получить несколькими различными способами, используя при этом одну и ту же общую решетку и одинаковые инициаторы. Кроме того, предположим, что существуют, по крайней мере, два генератора, которые дают одинаковый общий контур фигуры. Теперь можно легко рандомизировать построение, случайным образом выбирая на каждом этапе один из двух упомянутых генераторов. Генераторы могут, например, выглядеть вот так:
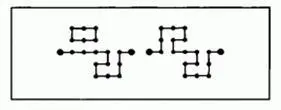

Рис. 322. Случайное побережье Коха (размерность D=1,6131 )
Общая форма случайного острова Коха, построенного таким способом, сильно зависит от исходной фигуры. В частности, все начальные симметрии явственно прослеживаются на любом из этапов построения. По этой причине (равно как и по другим, описанным в главе 24) метод построения случайной кривой Коха путем случайной перетасовки ее элементов имеет весьма ограниченную область применения.

Рис. 323. Случайная кривая Пеано (размерность D=2 )
Изображенный ниже генератор вкупе с инициатором [0,1] дает в пределе кривую, заполняющую треугольник.
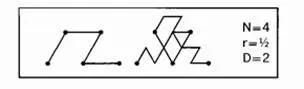
Положение и вид генератора определяется четностью номера интервала в терагоне. На интервалах с нечетными номерами вышеприведенный (т.е. прямой, S ) вариант генератора располагается справа от кривой. К интервалам же с четными номерами применяется обратный (F) вариант генератора, и располагается он слева от кривой. Суть метода рандомизации, результат которой показан на рисунке; состоит в том, что выбор этих фокальных точек производится случайным образом. В данном примере распределение симметрично относительно средней точки интервала. Каждый подтреугольник разбивается позднее на четыре подтреугольника, причем независимым от соседей образом, и процесс продолжается до бесконечности.
Для того чтобы за изменениями терагона было легче проследить, каждый интервал заменен двумя, причем добавочная концевая точка является серединой «крыши» этого интервала.
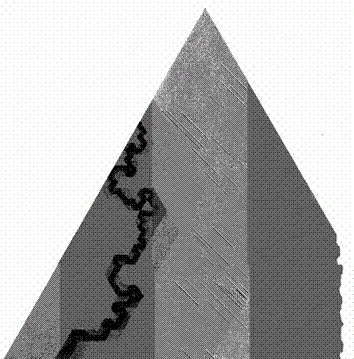
Рис. 324. Треугольник и сквиг — кривая
Здесь проиллюстрировано поэтапное построение простейшей сквиг – кривой – каждый последующий этап совмещен с предыдущим и показан более темным оттенком серого цвета. Обратите также внимание на следующее обстоятельство: то, что мы не видим светлого оттенка под темным, не означает, что светлая область в этом месте прерывается. Начинается построение светло-серым треугольником, а заканчивается кривой черного цвета. Масштаб изображения этапов с 6 по 10 несколько больше масштаба для этапов с 0 по 5. Сами этапы описаны в тексте главы.

Рис. 325. Шестиквиговая береговая линия
На этом рисунке изображены шесть сквиг – кривых, соединенных концами и образующих петлю без самопересечений. Размерность фигуры очень близка к D=4/3 . Это же значение фигурирует и во многих других примерах кривых без самопересечений – например, границы броуновской оболочки на рис. 341, сходство которой с нашим «шестисквигом», безусловно, заслуживает упоминания.
25 БРОУНОВСКОЕ ДВИЖЕНИЕ И БРОУНОВСКИЕ ФРАКТАЛЫ
Интервал:
Закладка:








![Пьер Бенуа - Атлантида. Забытый. Прокаженный король. Владелица ливанского замка. Кенигсмарк. Дорога гигантов. Соленое озеро [компиляция]](/books/1088284/per-benua-atlantida-zabytyj-prokazhennyj-korol.webp)

