Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями

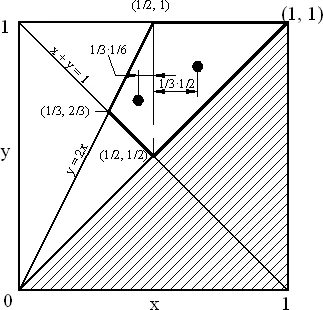
Рис. 21. Область, где X отвечает наибольший кусок.

Рассмотрим теперь случай, когда X — наибольший кусок. Тогда

X > Y − X , или 2 X > Y

и

X > 1 − Y , или X + Y > 1.

На рис. 21 изображен соответствующий четырехугольник. Для того чтобы найти координату X его центра тяжести, разобьем его на два треугольника по пунктирной линии. Затем вычислим среднее этих координат для каждого треугольника и сложим их с весами, равными площадям треугольников.

Среднее значение X для правого треугольника равно 1/2 + 1/3·1/2, для левого треугольника 1/2 − 1/3·1/6. Площади треугольников пропорциональны 1/2 и 1/6 так как у них одно и то же основание. Таким образом, среднее для величины X есть

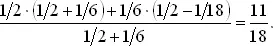
Так как среднее значение длины самого маленького куска равно 1/9 или 2/18, а самого длинного 11/18, то для среднего куска оно оказывается равным 1 − 11/18 − 2/18 = 5/18. Этот факт нетрудно получить и непосредственным подсчетом, рассмотрев область, соответствующую неравенствам 1 − Y > X > Y − X .

Итак, средние длины короткого, среднего и длинного кусков относятся как 2 : 5 : 11.

Если ломать стержень на две части, то средние дайны короткого и длинного кусков относятся как

1/4 : 3/4 или 1/2 · 1/2 : 1/2 · (1/2 + 1).

Для трех кусков мы получили пропорцию

1/9 : 5/18 : 11/18,

что можно записать в виде

1/3 · 1/3 : 1/3 · (1/3 + 1/2) : 1/3 · (1/3 + 1/2 + 1).

В общем случае разламывания стержня на n кусков средние длины равны:

наименьший кусок

второй по длине кусок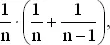

третий по длине кусок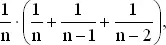

. . . . . . . . . . . . . . . . . . . . .

наибольший кусок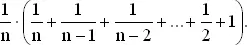

Автор, к сожалению, не располагает простым доказательством этого факта.

Не стоит расстраиваться из-за того, что игра несправедлива, ведь в конце концов только вы можете получить приз. Пусть ваш партнер для краткости обозначен через B , вы — через A . Пусть также общее число партий равно N = 2 n . Вероятность выигрыша в каждой отдельной игре равна p , а проигрыша q = 1 − p .

Первая мысль, приходящая в голову многим, состоит в том, что поскольку игра не безобидна, то с возрастанием N средняя разность (число очков A минус число очков B ) становится все «больше отрицательной». Отсюда делается вывод о том, что A должен играть как можно меньше игр, т. е. две игры.

Если бы правилами допускалось нечетное число игр, то это соображение действительно привело бы к правильному результату, и A должен был бы играть всего одну игру. Для четного же числа игр накладываются два эффекта: (1) смещение в пользу В и (2) изменение среднего члена биномиального распределения (вероятности ничьей) с ростом числа сыгранных партий.

Рассмотрим на минуту справедливую игру ( p = 1/2). Тогда чем больше N , тем больше вероятность победы A , так как при возрастании 2 n вероятность ничьей стремится к нулю, и вероятность выигрыша A стремится к 1/2. Для N = 2, 4, 6 эти вероятности равны соответственно 1/4, 5/16, 22/64. Из соображений непрерывности следует, что при p незначительно меньшем, чем 1/2, A следует выбирать большое, но конечное число игр. Однако, если p мало, то выбор N = 2 является оптимальным для A . Оказывается, что это так в случае, когда p < 1/3.

Вероятность выигрыша в игре, состоящей из 2 n партий, равна сумме вероятностей получения n + 1, n + 2, ..., 2 n очков, т. е.

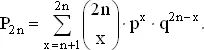
Если играются 2 n + 2 туров, то вероятность выигрыша равна

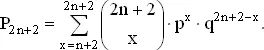
Игра, составленная из 2 n + 2 партий, может быть рассмотрена как игра из 2 n туров с добавлением еще двух туров. Если только игрок A не набрал n или n + 1 очко в игре из 2 n туров, то он остается выигравшим или проигравшим в игре из 2 n + 2 партий в зависимости от того, выиграл он или проиграл в игре из 2 n партий.

Итак, вычислим (1) вероятность получения n + 1 очка в первых 2 n партиях и проигрыша в следующих двух, равную

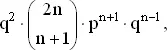
и (2) вероятность получения n очков в первых 2 n партиях и выигрыша в следующих двух, которая равняется

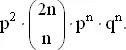
Если N = 2 n — оптимальный выбор для A , то P N − 2≤ P N , P N ≥ P N + 2. Из предыдущих рассуждений следует, что эти неравенства эквивалентны следующим:

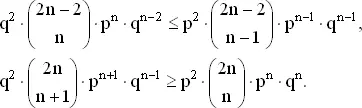(1)

После незначительных преобразований (при которых исключается тривиальный случай p = 0) неравенства (1) сводятся к следующим:

( n − 1)· q ≤ np , nq ≥ ( n + 1)· p . (2)

Отсюда выводим

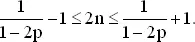
Итак, если только 1/(1 − 2 p ) не является нечетным числом, то значение N определяется единственным образом, как ближайшее четное число, меньшее 1/(1 − 2 p ). Если же 1/(1 − 2 p ) нечетное число, то для обоих четных чисел 1/(1 − 2 p ) − 1 и 1/(1 − 2 p ) + 1 оптимальные вероятности одни и те же, т. е. если

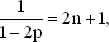
то

P 2 n = P 2 n + 2.

Для p = 0.45 в качестве оптимального числа партий получаем 1/(1 − 0.9) = 10.

Рассмотрим сначала задачу с колодой карт. Если в колоде 52 карты, то каждая карта с вероятностью 1/52 занимает место, уже занятое такой же картой. Так как общее число возможных мест для каждой карты равно 52, то среднее число совпадений равно 52·1/52 = 1. Таким образом, в среднем происходит только одно совпадение. Если бы колода состояла из n различных карт, то среднее число совпадений прежнему равнялось бы 1, так как n ·(1/ n ) = 1. Этот вывод основывается на теореме о том, что среднее суммы есть сумма средних.