Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями

Рис. 10.

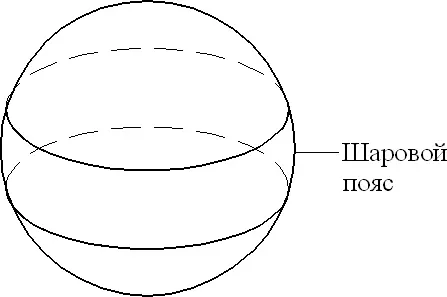
Рис. 11.

На поверхности сферы выбирается случайная точка, и если радиус, проведенный из центра в эту точку, пересекает боковую поверхность цилиндра, то считается, что монета упала на ребро.

На практике этой ситуации отвечает клейкая поверхность, мягко упав на которую монета опускается либо на ребро либо на одно из оснований (рис. 12).

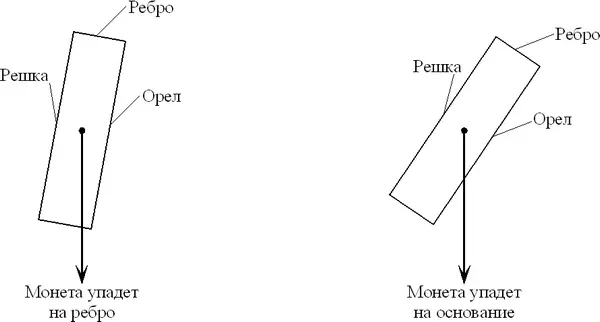
Рис. 12.

Для решения задачи нам понадобится следующий результат. Поверхность куска сферы, заключенного между двумя параллельными плоскостями, пропорциональна расстоянию между этими плоскостями, так что толщина нашей монеты должна составлять 1/3 диаметра сферы. Дадим окончательный ответ в терминах диаметра монеты (рис. 13).

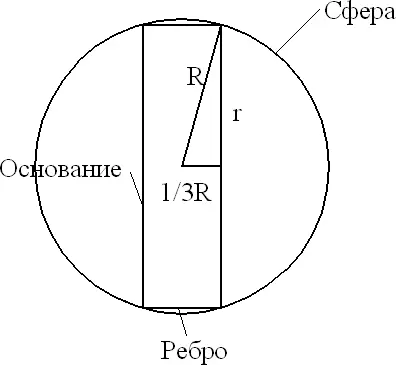
Рис. 13. Чертеж сечения сферы, поясняющий соотношение между радиусом R сферы и радиусом r монеты.

Пусть R — радиус сферы, а r — радиус монеты. Согласно теореме Пифагора

Итак, высота ребра монеты составляет около 35% ее диаметра.

Предположим, что несколько точек брошены случайным образом на отрезок [0, 1]. Например, пусть это точки w , x и y , как показано на рис. 14.

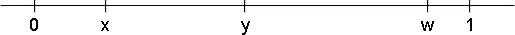
Рис. 14. Три точки на единичном отрезке.

Эти три точки делят наш отрезок на четыре части с длинами х , у − х , w − y , 1 − w . Если процедура бросания повторяется, то по-прежнему мы получаем четыре отрезка (левый, второй, третий и правый), и можно поставить вопрос о распределении длины, скажем, левого промежутка. Фиксируем некоторое число t . Какова вероятность того, что все три точки упадут справа от t ? Так как бросания независимы, и вероятность того, что каждая точка упадет справа от t , равна 1 − t , то ответом на поставленный вопрос является (1 − t )³.

Итак,

P (левая точка лежит справа от t ) = (1 − t )³.

Пример.Какова медиана распределения левой точки? Медианой распределения называется точка, вероятность падения слева от которой равняется 1/2.

Имеем (1 − t )³ = 1/2,

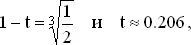
В то время как распределение длины левого промежутка находится просто, а распределение длины правого из соображений симметрии совпадает с распределением левого, задача нахождения распределения длин второго и третьего промежутков может представить известные трудности. Может быть, читатель уже догадался, что эти распределения равны распределению длины левого промежутка, но так, впрочем, думают совсем немногие. Целью следующих замечаний и является разъяснение этого факта.

Вместо того, чтобы бросать точки на единичный отрезок, будем бросать их на окружность единичной длины. При этом вместо трех точек используем четыре, причем четвертую точку обозначим через z (рис. 15).

Рис. 15. Четыре точки на единичной окружности.

Таким образом, точки x , y и w , как и раньше, размещены на единичном интервале, у которого, однако, случайные концы. В силу равноправности всех четырех точек длины дуг ( z , x ), ( x , y ), ( y , w ) и ( w , z ) имеют одно и то же распределение. Если процесс бросания производится несколько раз, и при каждом бросании вычисляется длина дуги от точки z до следующей против часовой стрелки, от этой — так же до следующей и т. д., то имеет смысл говорить о распределении длин этих дуг, причем для всех дуг это распределение одинаково.

Разрывая окружность в точке z и разворачивая ее в отрезок, видим, что бросание четырех течек на окружность, одна из которых используется как начало отсчета, эквивалентна бросанию трех точек на единичный интервал.

Мы не дадим здесь строгого доказательства, хотя читатель, быть может, и не вполне убежден предыдущими рассуждениями. Верен общий принцип симметрии:

Принцип симметрии. При бросании n точек наудачу на отрезок, распределение длин n + 1 получающихся при этом отрезков одинаково.

В предположении того, что трубка разбивается случайно, из принципа симметрии выводим, что распределение длины каждой части с красной меткой, средней и с синей меткой одинаково и, значит, равны и их математические ожидания. Так как сумма этих величин постоянна и равна 9 см , то средняя длина куска трубки с красной меткой равна 3 см .

Естественно считать, что принцип симметрии сохраняется и для дискретных распределений. Четыре туза делят колоду на 5 частей, каждая из которых содержит от 0 до 48 карт. Если два туза лежат подряд, то будем говорить, что длина соответствующего куска колоды равна нулю. Аналогично нулевую длину имеют части колоды, которые находятся до первого туза, если он лежит сверху, и за четвертым тузом, если он является последней картой в колоде. Согласно принципу симметрии средняя длина каждой части равна 48/5 = 9.6. Последующей картой должен быть туз, который является, таким образом, в среднем 10.6 картой.

Хотя на поставленные вопросы вряд ли можно дать «правильный» ответ, все же возможно разумное объяснение этих задач. Например, согласно принципу симметрии, если на отрезок бросается одна точка, то в среднем два полученных отрезка имеют одинаковую длину, так что в пункте (а) ответ равен 119, так как длина левого промежутка равна 59, 2·59 = 118 и 118 + 1 = 119.

Аналогично в пункте (б) можно предположить, что пять наблюденных номеров разбивают весь отрезок на шесть равных частей. Так как 60 − 5 = 55, то средняя длина первых пяти отрезков равна 11, и общее число номеров может быть оценено как 60 + 11 = 71 (рис. 16). Конечно, оценка не может быть абсолютно точной при многократном употреблении.