Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями

P ₁ = 1 − p + p · P ₂, (1)

так как 1 − p есть вероятность поглощения на первом шаге и p · P ₂ — вероятность поглощения на последующих шагах.

Каждый путь, ведущий к поглощению из x = 2, можно разбить на две части:

(1) Путь, идущий из точки x = 2 и достигающий положения x = 1 в первый раз (не обязательно за один шаг) и

(2) Путь, идущий из точки x = 1 в точку x = 0 (также не обязательно за один шаг). Вероятность пути из положения x = 2 в x = 1 есть P ₁ поскольку структура блуждания здесь идентична структуре первоначального блуждания (см. рис. 35.1), за исключением того, что начало координат переносится на один шаг направо. Вероятность попасть из точки x = 1 в x = 0 также равна P ₁ как и в исходной задаче. Величина P ₂ поэтому есть P ₁², так как события A (частица идет по пути от точки x = 2 к x = 1) и B (частица движется по пути от точки x = 1 до x = 0) независимы, и P ( A ) = P ( B ) = P ₁.

Мы можем переписать уравнение (1) как

P ₁ = 1 − p + p · P ₁², (2)

Уравнение (2) — квадратное относительно P ₁ и имеет два решения:

P ₁ = 1; P ₁ = (1 − p )/ p . (3)

В таких задачах одно или оба решения могут быть подходящими, в зависимости от значений p .

Если p = 1/2, то оба решения совпадают, и P ₁ = 1. Когда p = 1, P ₁ = 0, так как частица всегда движется вправо. И когда p = 0, очевидно, P ₁ = 1. При p < 1/2 второе решение (3) не подходит, так как тогда (1 − p )/p > 1, а по смыслу задачи P ₁ ≤ 1. Поэтому при 0 ≤ p ≤ 1/2 мы имеем P ₁ = 1.

Чтобы доказать, что второе решение P ₁ = (1 − p )/ p имеет место при p > 1/2, нам достаточно установить, что P ₁ является непрерывной функцией от p (грубо говоря, что P ₁ не слишком изменяется, когда p меняется мало). Мы предполагаем эту непрерывность, но не доказываем ее.

Кривая (см. рис. 8) начинается в точке P ₁ = 1 при p = 1/2; она должна спуститься к P = 0 при p = 1, и ее ордината всегда должна равняться 1 или (1 − p )/ p . Кривая не имеет разрывов только в том случае, когда при p > 1/2 соответствующее значение равно (1 − p )/ p . Итак, при предположении непрерывности функции P ₁ мы получаем P ₁ = (1 − p )/ p при p > 1/2. Поэтому наш пьяница с вероятностью 1/2 упадет вниз.

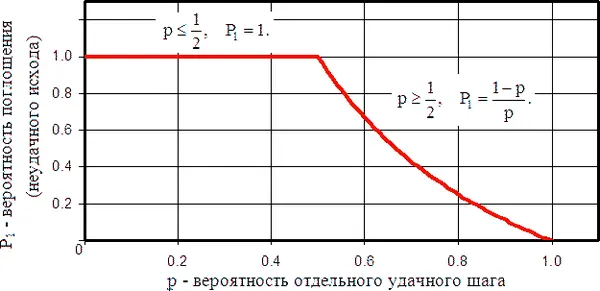
Рис. 8. Вероятности поглощения P .

Приведем другую интерпретацию. Рассмотрим игрока, имеющего начальный капитал в одну денежную единицу ( x = 1). Он может играть неограниченно долго, причем в каждом туре игры он с какими-то вероятностями выигрывает или проигрывает эту единицу. Чтобы вероятность банкротства игрока была не более 1/2, вероятность выигрыша в отдельной партии должна быть не менее 2/3. То, что банкротство неизбежно при p = 1/2, для большинства из нас неожиданность.

Приведем еще один взгляд на задачу. Рассмотрим игрока с начальным капиталом x = 1, играющего неограниченно долго против казино с бесконечным капиталом в «безобидную игру» ( p = 1/2), при которой он выигрывает или проигрывает единицу в каждом туре. Он наверное обанкротится ( P ₁ = 1). Чтобы он не стал банкротом с вероятностью 1/2, вероятность его выигрыша в каждой отдельной партии должна быть p = 2/3. То, что банкротство неизбежно при p = 1/2, является неожиданным для большинства из нас. Обычно считают, что если отдельные партии «безобидны» (средняя потеря равна нулю), то и вся игра безобидна. Разумеется, это представление в обычном смысле верно. Если мы представим такую игру с p = 1/2 и большим числом партий, то среднее значение денежной суммы на руках после n туров равно 1 для каждого конечного числа n . Таким образом, отсутствие «безобидности» является одним из парадоксов бесконечного.

Другой удивительный факт состоит в том, что при p = 1/2 среднее число шагов, требуемое для поглощения, бесконечно. Случай p = 1/2 является странным и глубоким.

Вас может заинтересовать применение указанного здесь метода к частице, выходящей из точки x = m , а не из точки x = 1. Обобщение приведенного выше результата, показывает, что вероятность поглощения с абсциссы x = m есть [(1 − p )/ p ] m или 1, в зависимости от того, будет ли p больше или меньше 1/2. Если p > 1/2 и m велико, то весьма вероятно, что частица избежит поглощения, и поэтому вероятность поглощения мала, а не равна 1.

Если частица выходит из начала координат 0 и ей разрешается делать шаги в обоих направлениях с вероятностью p = 1/2, то в другой классической задаче о блуждании ставится вопрос о том, вернется ли частица когда-либо в начало координат. Мы уже видели, что так действительно будет, ибо она заведомо вернется из положений x = 1 и x = −1. Дальнейшие сведения об этой задаче будут сообщены ниже.

Наша задача — специальный случай общей задачи о случайном блуждании с двумя поглощающими барьерами. Исторически эта проблема была поставлена как игровая, называемая задачей о разорении игрока, и многие знаменитые математики занимались вопросами, связанными с ней. Сформулируем задачу в общем виде.

Игрок M имеет m денежных единиц, игрок N — n единиц. После каждой игры один игрок выигрывает, другой проигрывает единицу. В каждой партии вероятность выигрыша игрока M равна p , а выигрыша N равна q = 1 − p . Игра продолжается до разорения одного из игроков. На рис. 36.1 указана сумма денег, которую игрок M имеет в настоящий момент. Он начинает с положения x = m . Когда x = 0, он разорен, при x = m + n банкротом является игрок N .

Рис. 36.1. Схематическое изображение задачи о разорении игрока

При такой постановке, поскольку p > 1/2, мы можем использовать результат задачи 35. Мы уже знаем, что если игрок M играет против банка с неограниченными ресурсами, то становится банкротом с вероятностью ( q / p ) m. По пути к банкротству он либо получает сумму m + n ( n теперь конечно) либо никогда не будет иметь ее на руках. Пусть вероятность того, что он проиграет игроку N , равна Q (это событие равносильно выигрышу N у банка с неограниченным капиталом без достижения игроком M суммы m + n ). Тогда

( p / q ) m = Q + (1 − Q )·( q / p ) m + n , (1)