Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями
- Название:Пятьдесят занимательных вероятностных задач с решениями
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями краткое содержание
Книга обращена к широкому кругу читателей: ученикам старших классов, педагогам, студентам.
Пятьдесят занимательных вероятностных задач с решениями - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
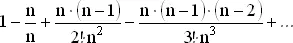 (1)
(1)
Если мы исследуем поведение каждого слагаемого, скажем, четвертого, то заметим, что при росте n оно стремится к −1/3!, так как
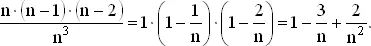 (2)
(2)
При n , стремящемся к бесконечности, все слагаемые в правой части (2), кроме 1, стремятся к нулю. Аналогично, для r -го слагаемого разложения (1) множитель, зависящий от n , стремится к единице, а все слагаемое с точностью до знака, к 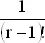
Таким образом, с ростом r выражение 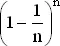 стремится к сумме ряда
стремится к сумме ряда
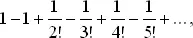
который является одним из способов вычисления e −1.
Если бы в каждом ящике было две фальшивые монеты, то искомая вероятность, равная 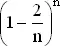 , сходилась бы при больших n к e −2и, точно так же,
, сходилась бы при больших n к e −2и, точно так же, 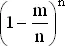 стремится к e −m . Вообще
стремится к e −m . Вообще 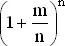 стремится к e m при любом (целом или нет) значении m . Эти факты будут использованы в дальнейшем. Более строгое их обоснование можно найти в любом учебнике по дифференциальному исчислению.
стремится к e m при любом (целом или нет) значении m . Эти факты будут использованы в дальнейшем. Более строгое их обоснование можно найти в любом учебнике по дифференциальному исчислению.
28. Решение задачи о жадном фальшивомонетчике
Каждая из проверяемых монет изымается из нового ящика и с вероятностью m / n фальшива. Так как монеты извлекаются независимым образом, то искомая вероятность отвечает биномиальному распределению.
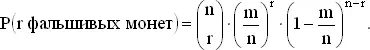
Исследуем поведение этой вероятности при возрастании n и фиксированных r и m .
Для этого запишем ее в виде
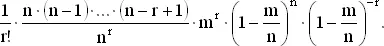
С ростом n 1/ r ! и m r не меняются, а
n ·( n − 1)· ... ·( n − r + 1)/ n r стремится к 1, как указано в задаче 27, 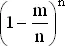 стремится к e −m и
стремится к e −m и 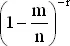 стремится к 1 (так как m и r фиксированы). Поэтому при больших n
стремится к 1 (так как m и r фиксированы). Поэтому при больших n
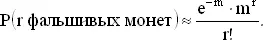
Сумма этих вероятностей равна:
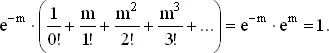
Ряд, записанный в скобках, является разложением e m .
Распределение, задаваемое вероятностями

называется законом Пуассона и служит хорошей математической моделью для многих физических процессов.
29. Решение задачи о заплесневевшем желатине
Разобьем поверхность пластинки на n малых равных площадок. Для каждой площадки вероятность колонии равна p , а их среднее число есть np = 3. Нас интересуют лишь маленькие площадки. Когда n растет, p становится малым, так как площадь участков стремится к нулю. Вместо того, чтобы считать среднее число колоний равным 3, будем рассматривать общее среднее m = np . Может показаться, что на некоторых площадках встречаются две или больше колоний, но эти сомнения можно оставить, потому что площадки столь малы, что едва умещают одну колонию. Тогда вероятность ровно r колоний на n маленьких площадках равна
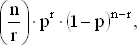
где p = m / n . Заменим p на m / n в этой формуле. Полученное выражение уже знакомо нам по задаче 28. Пусть n → ∞. Тогда мы снова приходим к распределению Пуассона

При m = 3 и r = 3 получаем значение 0.224.
То, что m действительно является средним этого распределения, проверяется непосредственно:
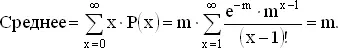
Чтобы получить численные результаты для больших значений m , где r = m , можно использовать таблицы [10] См., иапример, Л. Н. Большев, Н. В. Смирнов, Таблицы математической статистики «Наука», 1965, стр. 360 (прим. перев.) .
или формулу Стирлинга. Последняя дает

| m | P ( m ) | 0,4√ m |
| 4 | 0.1954 | 0.200 |
| 9 | 0.1318 | 0.133 |
| 16 | 0.0992 | 0.100 |
30. Решение задачи о расчете булочника
Почему мы пользуемся предположением о распределении Пуассона? Отчасти потому, что задача допускает тогда красивое решение, а отчасти потому, что распределение действительно может быть близким к пуассоновскому, так как булочник имеет много клиентов, каждый из которых довольно редко покупает кекс. Если читателя беспокоит колебание числа покупок, связанное с разными днями недели, то будем говорить лишь о вторниках в течение лета.
Большинство обычно считает, что искомая вероятность равна 1/2.
Вероятность продать ровно r кексов есть e −20·20 r / r !, как известно из задачи 28. Заменив 20 на m , мы лучше выясним структуру задачи. Сумма вероятностей закона Пуассона есть ∑ e − m · m r / r ! или
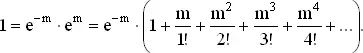 (A)
(A)
Нашей целью является выделение слагаемых, отвечающих нечетным количествам покупок. Известно, что
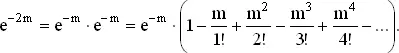 (B)
(B)
Интервал:
Закладка:










