Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями

По существу, вопрос состоит в определении числа возможных случаев в задаче о парных днях рождения. В задаче об индивидуальном дне рождения для n людей имеется n возможностей встретить человека, день рождения которого такой же, как у вас. В задаче о парных днях рождения каждый человек сравнивает свой день рождения с r − 1 днями рождения остальных людей. Число пар равно, таким образом, r ·( r − 1)/2, что и является числом возможных случаев. Для того чтобы вероятности в двух задачах приблизительно равнялись, должно выполняться соотношение

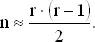(1)

Например, при r = 23 число n должно равняться 23·22/2 = 253, что согласуется с полученным ранее.

Мы уже видели, что при n значительно меньшем по сравнению с N , вероятность того, что ни один из n людей не родился с вами в один и тот же день, приближенно равна e − n / N . С другой стороны, в задаче о парных днях рождения было показано, что для значений r , малых по сравнению с N , вероятность отсутствия парных дней рождения приблизительно равна e − r ·( r − 1)/2 N . Для равенства этих двух вероятностей должно иметь место соотношение (1). Полученная аппроксимационная формула поясняет связь этих двух задач. Из сказанного ранее следует, что r ·( r − 1)/2 имеет смысл числа возможных случаев, что также дает основание для сопоставления n и r ·( r − 1)/2.

Если на фабрике работает один человек, то предприниматель получает 364 человеко-дней, если два, то почти всегда 2·363 = 726, так что можно думать, что максимум достигается при числе рабочих, большем двух. С другой стороны, при весьма большом числе рабочих практически каждый день является выходным, и завод никогда не работает. Следовательно, действительно существует конечное число рабочих, на котором достигается максимум.

Найдем среднее число рабочих дней. Каждый день является либо рабочим либо нет. Заменим для общности 365 на N и обозначим через n число рабочих на фабрике. Тогда вероятность того, что первый день в году — рабочий, равна (1 − 1/ N ) n , так как в этом случае все рабочие родились в один из других N − 1 дней. Средний вклад первого дня в трудоднях равен

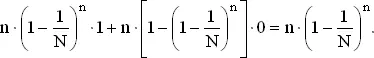
Это число одинаково для всех дней, так что среднее число человеко-дней, отработанных в году, при n рабочих на фабрике равно n · N ·(1 − l/ N ) n . Для максимизации этой функции от n надо найти значение n , для которого

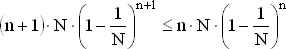
и

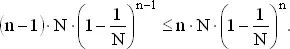
Первое неравенство означает, что

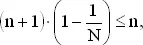
или

N ≤ n + 1.

второе, что

Отсюда получаем n ≤ N ≤ n + 1 и, значит, или n = N , или же n = N − 1. Подставляя эти значения n в формулу для среднего числа человеко-дней, мы получаем N ²·(1 − 1/ N ) N и ( N − 1)· N ·(1 − 1/ N ) N − 1 т. е. равные величины. Так как N -й человек не изменяет положения дел, на фабрике должно быть N − 1 рабочих. В силу соотношения (1 − 1/ N ) N ≈ e −1среднее число трудодней приблизительно равно N ²· e −1. Если бы все N человек работали каждый день, то число трудодней равнялось бы N ², так что e −1равняется среднему отношению числа действительно проработанных дней к потенциально возможному N ². Оно приблизительно равно 0.37. Итак, на фабрике работает 364 человека, и число рабочих дней приблизительно равно 49 (если считать, что других выходных нет). 364-й рабочий вкладывает в среднем только 0.37 дня в общее число трудодней. Рабочая сила должна быть очень дешева в этом городе!

Перед решением задачи полезно задуматься о возможном ответе. Посмотрим, что может случиться на нескольких первых шагах. Приведенная схема иллюстрирует тот факт, что человек может упасть вниз только через нечетное число шагов. После одного шага вероятность упасть вниз равна 1/3 (рис. 6). Путь 1 → 2 → 1 → 0 добавляет еще 2/27 к вероятности падения, давая общую вероятность несчастья 11/27. После пяти шагов пути 1 → 2 → 1 → 2 → 1 → 0 и 1 → 2 → 3 → 2 → 1 → 0 вместе добавляют 8/243 к вероятности падения, давая общий результат 107/243. Этот список можно продолжить, но мы обратимся теперь к иному подходу.

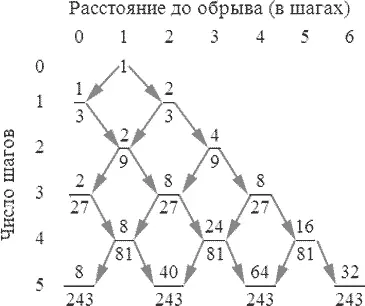
Рис. 6. Схема блуждания пьяницы, показывающая вероятность нахождения на различных расстояниях от края пропасти.

Настоящая задача о блуждании весьма популярна и имеет много формулировок. Далее мы будем трактовать ее как задачу о частице, движущейся по оси.

Рассмотрим частицу, которая сначала находится в положении x = 1 на оси. Структура задачи будет яснее, если вероятность шага направо вместо 2/3 будет равна p . Частица движется из положения 1 либо в точку x = 2 с вероятностью p , либо в точку x = 0 с вероятностью 1 − p (рис. 7). Вообще, если частица находится в положении x = n , n > 0, n — целое число, то она сдвигается либо в точку x = n + 1 с вероятностью p , либо в точку x = n − 1 с вероятностью 1 − p . Если частица попадает в положение x = 0, то там она поглощается (не делает других шагов). Нас интересует значение вероятности P ₁ того, что частица поглощается в точке x = 0, если она выходит из точки x = 1. Разумеется, значение P ₁ зависит от p . Кажется естественным, что если p близко к 1, то вероятность P ₁ мала, а если p близко к нулю, то P ₁ мало отличается от 1.

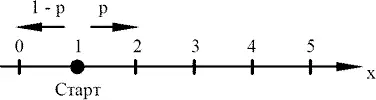
Рис. 7.

Рассмотрим ситуацию после первого шага: либо частица сдвинулась налево, попала в точку x = 0 и поглотилась там (это событие имеет вероятность 1 − p ), либо сдвинулась направо в точку x = 2 (это событие происходит с вероятностью p ). Пусть P ₂ обозначает вероятность того, что частица поглощается в начале координат x = 0, если она выходит из точки x = 2. Тогда мы имеем