Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями

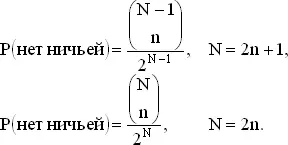
Эти формулы показывают, что указанная вероятность одна и та же для четного N и для следующего за ним нечетного числа N + 1. Например, когда N = 4, надо применить вторую формулу. Шестнадцатью возможными исходами являются

ААAA BAAA ABBA BABB

*AAAB AABB BABA *BBAB

*AABA ABAB BBAA *BBBA

ABAA BAAB ABBB *BBBB

где звездочкой отмечены комбинации с равновесным положением.

Поскольку число сочетаний из 4 по 2 равно 6, то вторая формула действительно верна для этого значения N .

При N = 2 n вероятность x выигрышей A есть 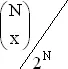. Если x ≤ n , то вероятность ничьей есть 2 x / N (на основании задачи 22), а при x ≥ n эта вероятность равна 2·( N − x )/ N . Чтобы получить вероятность ничьей, находим вероятность x выигрышей, умножим ее на условную вероятность ничьей при x выигрышах и просуммируем полученные выражения, что дает

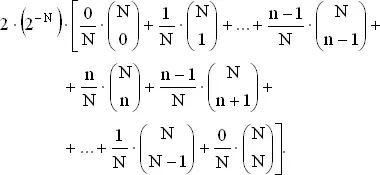(1)

Если подставить в это выражение формулу для биномиальных коэффициентов и произвести необходимые сокращения, то с точностью до слагаемого

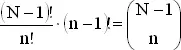
получим 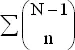, где суммирование ведется по всем возможным значениям x . Следовательно, мы можем переписать выражение (1) в виде

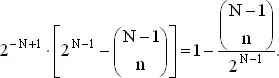(2)

Отсюда видно, что вероятность отсутствия ничьей есть

,

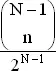что после небольших преобразований может быть записано в виде

,

как было указано выше.

Поезда в направлении к невесте останавливаются у перрона, куда приходит Мэрвин, скажем, в 3 00, 3 10, 3 20и т. д., поезда в противоположном направлении в 3 01, 3 11, 3 21и т. д. Чтобы поехать к матери, Мэрвин должен попасть в одноминутный интервал между поездами указанных типов.

Пока выражение «наудачу» не уточнено, задача не имеет определенного ответа. Следующие три возможных предположения с соответствующими тремя различными вероятностями иллюстрируют неопределенность понятия «наудачу», часто встречающуюся в геометрических задачах. Мы не можем гарантировать, что эти результаты должны согласовываться с некоторым физическим процессом, который мог бы быть использован для выбюра случайных хорд. Иначе задача могла бы быть проверена эмпирически.

Пусть радиус круга равен r .

(а). Допустим, что расстояние хорды от центра круга равномерно распределено между 0 и r . Поскольку правильный шестиугольник со стороной r можно вписать в круг, для определения искомой вероятности найдем расстояние d стороны этого шестиугольника от центра и разделим на величину радиуса. Заметим, что d — высота правильного треугольника со стороной r . Из планиметрии известно, что

Следовательно, искомая вероятность равна

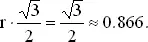
(б). Пусть середина хорды равномерно распределена во внутренности круга. Из чертежа (рис. 4) видно, что хорда длиннее радиуса, когда середина хорды находится на расстоянии, меньшем d , от центра. Таким образом, все точки круга радиуса d , концентрического с исходным кругом, являются геометрическим местом точек середины хорд. Площадь этого круга, деленная на площадь исходного, равна

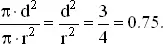
Эта вероятность равна квадрату выражения, полученного в случае (а).

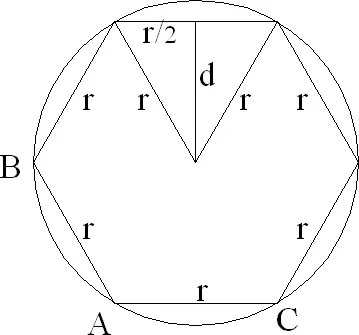
Рис. 4.

(в). Допустим, что хорда определяется двумя точками на окружности исходного круга. Пусть первая точка попала в A (рис. 4). Для того чтобы хорда была короче радиуса, вторая точка должна попасть на дугу BAC , длина которой есть 1/3 длины окружности. Следовательно, вероятность того, что хорда длиннее радиуса, равна 1 − 1/3 = 2/3.

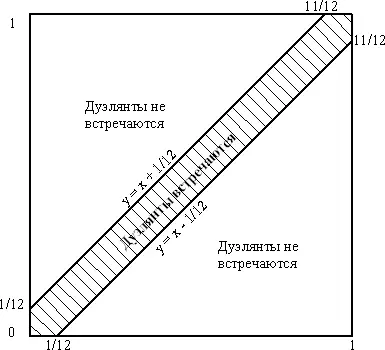
Рис. 5.

Пусть x и y обозначают время прибытия 1-го и 2-го дуэлянтов соответственно, измеренное в долях часа, начиная с 5 часов. Заштрихованная площадь квадрата (рис. 5) отвечает случаю, когда дуэлянты встречаются. Вероятность того, что они не встретятся, равна (11/12)², так что шансы на поединок равны 23/144 ≈ 1/6.

(а)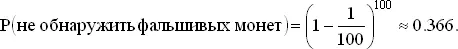

(б). Пусть имеется n ящиков, каждый из которых содержит n монет. Тогда вероятность того, что извлеченная наудачу монета доброкачественна, равна 1 − 1/ n , и так как всего имеется n ящиков, то

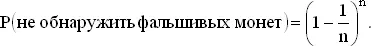
Вычислим эту вероятность для некоторых значений n .

Бросаются в глаза следующие два обстоятельства. Во-первых, выписанные в таблице числа с ростом n возрастают. Во-вторых, они стремятся к некоторому значению, которое известно математикам и равно e −1или 1/ e , где e = 2,71828... — основание натуральных логарифмов.

Воспользовавшись формулой бинома Ньютона для 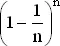, получим следующее выражение:

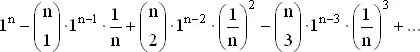
или