Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями

P + RP + R ² P + ... = P (1 + R + R ² + ...)

или

вероятность получить «пойнт» = P /(1 − R ).

Например, если «пойнт» равен 4,

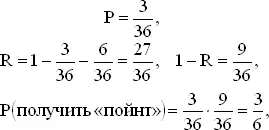
что согласуется с полученным ранее.

Сам автор решал сначала эту задачу с помощью суммирования бесконечного ряда и был обрадован, когда несколько дней спустя обнаружил указанный здесь более простой подход.

Трудно сказать, какой предварительный взнос вы сочтете подходящим для себя. Хотя математическое ожидание выигрыша в первой игре равно пяти долларам, вы можете не захотеть платить взнос, близкий к 5 долларам, за право игры. Потеря 3 или 4 долларов может весьма много значить для игроков. Вы можете, например, предложить взнос, в 75 центов.

Кажется естественным, однако, что взнос для участия во второй игре должен быть по крайней мере таким же, как и для их первой игры. Цвет всегда может быть выбран случайным бросанием монеты, что дает 50 % шансов правильного решения и математическое ожидание выигрыша, равное 5 долларам. Кроме того, если вы располагаете информацией о склонностях вашего друга, то она может быть использована для увеличения вероятности выигрыша.

Большинство людей склонно скорее к первой игре, так как условия второй представляются им менее определенными. Автор обязан этой задачей Г. Райфа; последний сообщил ему, что идея задачи принадлежит Д. Элсбергу.

Автор не встречал еще ни одного человека, который загадал бы многозначное число, при этом, как правило, называют числа 1, 3 и 7. В большинстве случаев была выбрана единица, но встречались также 3 и 7.

Когда этот вопрос был задан моей дочери, она живо ответила: «Ну конечно же, им надо встретиться в самом известном месте Нью-Йорка». — «Прекрасно, но где же именно?» — спросил автор. «Откуда я знаю? Ведь мне всего девять лет».

Что же приходит в голову? Крыша здания Эмпайр Стейт Билдинг [7] Эмпайр Стейт Билдинг — одно из самых высоких зданий (449 м вместе с телебашней) в центре Нью-Йорка (прим. перев.) . , аэропорты, бюро справок на железнодорожных станциях, статуя Свободы [8] Статуя Свободы — маяк в виде бронзовой фигуры женщины с факелом в руке, расположенный на небольшом островке вблизи Манхэттена (прим. перев.) . , Таймс Сквер [9] Таймс Сквер — центральная площадь Нью-Йорка (прим. перев.) . . Статую Свободы следует исключить сразу же по выяснении того, как трудно до нее добраться. Аэропорты не подходят по причине их многочисленности и удаленности от города. Тот факт, что в городе два крупных вокзала, по-видимому, исключит и их. Остаются Эмпайр Стейт Билдинг и Таймс Сквер. Я бы выбрал Эмпайр Стейт Билдинг, потому что Тайме Сквер сейчас разросся до неопределенных размеров.

Автору кажется, что если бы свидание было назначено в Сан-Франциско или в Париже, решить эту задачу было бы легче.

Из всех задач, о которых пишут автору, настоящая доставила наибольшее количество писем.

Ошибка в рассуждении А состоит в том, что он не перечислил всех возможных событий должным образом. Выражаясь математически, узник неправильно построил пространство элементарных событий. Он считает, что опыт имеет три возможных исхода: освобождение пар AB , AC , BC с равными вероятностями. С точки зрения заключенного — это правильно построенное пространство элементарных событий для эксперимента, проводимого администрацией, которая освобождает двух узников из трех. Но эксперимент A включает еще один момент — ответ охранника. Возможные исходы для такого эксперимента и разумные вероятности для них будут:

1) A и B освобождаются, и охранник говорит B , вероятность 1/3.

2) A и C освобождаются, и охранник говорит C , вероятность 1/3.

3) B и C освобождаются, и охранник говорит B , вероятность 1/6.

4) B и C освобождаются, и охранник говорит C , вероятность 1/6.

Если на вопрос A охранник отвечает B , то апостериорная вероятность освобождения А равна вероятности исхода 1, деленной на сумму вероятностей исходов 1 и 3. Таким образом, вероятность освобождения A равна (1/3)/(1/3 + 1/6) = 2/3, так что математический расчет в конце концов отвечает здравому смыслу.

Из первой коробки мы достаем один купон. Далее, вероятность получить новый номер из второй коробки равна 4/5. Используя ответ задачи 4, видим, что приобретение нового номера потребует в среднем (4/5) −1= 5/4 коробок. Третий номер потребует (3/5) −1= 5/3, четвертый 5/2, пятый — 5 коробок.

Таким образом, среднее число коробок равно

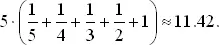
Хотя в данном случае указанные дроби сложить, но когда в комплекте большое число купонов, удобно применить формулу Эйлера для частичных сумм гармонического ряда:

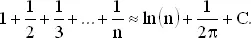
(Число C = 0.57721... называется постоянной Эйлера.) В случае комплекта из n купонов среднее число коробок приближенно равно

n ·log n + 0.577 n + ½.

Поскольку log 5 ≈ 1.6094, формула Эйлера при n = 5 дает 11.43, что весьма близко к 11.42. Членом 1/2 n в формуле Эйлера часто пренебрегают.

Например, если ряд заполнен следующим образом

BBMMBBMBMBMBBMM

(здесь B обозначает юношу, а M — девушку), то имеется 9 пар BM и MB .

Нас интересует среднее число таких пар. Если первые два места в ряду заняты лицами разных полов, то у нас уже имеется искомая пара. Вероятность этого события равна

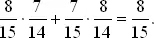
Более того, 8/15 есть и среднее число пар на первых двух местах, так как

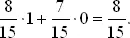
Такое же рассуждение применимо к каждой паре смежных мест.

Для определения среднего числа пар молодых людей эту величину надо умножить на число смежных мест, равное 14, что дает 112/15.

Более общим образом, если есть b объектов одного рода и m другого, располагаемых случайным образом в ряд, то среднее число пар, составленных из различных объектов, равно