Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями
- Название:Пятьдесят занимательных вероятностных задач с решениями
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями краткое содержание
Книга обращена к широкому кругу читателей: ученикам старших классов, педагогам, студентам.
Пятьдесят занимательных вероятностных задач с решениями - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
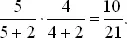
Это число близко к ½, но в условии задачи фигурирует ровно ½. Подойдем теперь к задаче алгебраически.
Пусть в ящике r красных и b черных носков. Вероятность того, что первый носок — красный, равна r /( r + b ) и при осуществлении этого события условная вероятность того, что второй вынутый носок также красный, есть ( r − 1)/( r + b − 1). Согласно условиям задачи вероятность того, что оба носка — красные, равняется ½, или
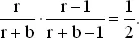
Можно начать со значения b = 1 и искать нужное значение r , затем перейти к случаю b = 2 и рассмотреть различные значения r и т. д. Это довольно быстро приводит к решению. Но можно подойти к задаче и на более солидном математическом уровне.
Заметим, что
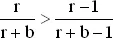 при b > 0.
при b > 0.
Отсюда следует неравенство
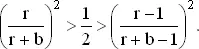
Извлекая квадратные корни, для r > 1 получаем
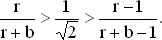
Из первого неравенства имеем
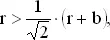
или
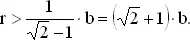
Из второго неравенства находим
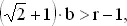
так что
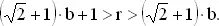
Для b = 1 получаем
2.414 < r < 3.414,
так что можно взять r = 3. При r = 3, b = 1 имеем
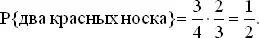
Таким образом, минимальное число носков есть 4.
Рассмотрим теперь четные значения b .
| b | r между | Подходящее r | P (2 красных носка) |
| 2 | 4,9; 5,8 | 5 | (5·4)/(7·6) ≠ 1/2 |
| 4 | 9,7; 10,7 | 10 | (10·9)/(14·13) ≠ 1/2 |
| 6 | 14,5; 15,5 | 15 | (15·14)/(21·20) = 1/2 |
Таким образом, минимальное число носков в ящике есть 21 при условии, что b четно. Если интересоваться всеми значениями r и b такими, что вероятность извлечения двух красных носков равна ½, то следует использовать методы теории чисел. Этот вопрос приводит к знаменитому уравнению Пелла [4] См., например, Б. В. Венков. Элементарная теория чисел, М., ГТИ, 1937 (прим. перев.) .
. Возьмите, например, r = 85, b = 35.
2. Решение задачи о последовательных выигрышах
Поскольку чемпион играет лучше отца, сыну следует играть с ним поменьше партий. С другой стороны, вторая партия — основная, так как сын не может выиграть дважды подряд, не выиграв вторую партию. Пусть C означает чемпиона, F — отца, W и L — выигрыш и проигрыш сына. Пусть, далее, f есть вероятность того, что сын выиграет у отца, а c — вероятность того, что он выиграет у чемпиона. Считается, что выигрыши сына независимы. В следующей ниже таблице приводятся возможные результаты и их вероятности.
| Схема FCF | Схема CFC | ||||||
| F | C | F | Вероятности | C | F | C | Вероятности |
| W | W | W | fcf | W | W | W | cfc |
| W | W | L | fc(1 − f) | W | W | L | cf (1 − c ) |
| L | W | W | (1 − f ) cf | L | W | W | (1 − c ) cf |
| Общая вероятность выигрыша | fc (2 − f ) | Общая вероятность выигрыша | fc (2 − c ) |
Так как отец играет хуже чемпиона, f > c и (2 − f ) < (2 − c ), так что сыну нужно выбрать вариант CFC . Например, если f = 0.8, c = 0.4, то вероятность получить приз при схеме FCF равна 0.384, а при схеме CFC — 0.512. Таким образом, бо́льшая вероятность выигрыша второй партии перевешивает невыгоды игры два раза с чемпионом.
Многие предполагают, что чем больше математическое ожидание числа успехов, тем больше вероятность выиграть приз, и часто такой подход бывает правильным. Но в данной задаче есть условия, нарушающие такие рассуждения по аналогии.
Среднее число выигрышей по схеме CFC равно 2 c + f , и оно меньше, чем среднее число побед для схемы FCF , 2 f + c . В нашем числовом примере при f = 0.8 и c = 0.4 эти средние равны, соответственно, 2 и 1.6. Такое «противоречие» придает задаче специальный интерес.
3. Решение задачи о легкомысленном члене жюри
Оба типа жюри имеют одинаковую вероятность вынести правильное решение. В самом деле, два серьезных члена жюри будут голосовать за справедливое решение с вероятностью p · p = p ², при этом результат голосования третьего члена жюри не существен. Если же эти судьи расходятся во мнениях, вероятность чего равна p (1 − p ) + (1 − p ) p = 2 p (1 − p ), то для нахождения вероятности правильного решения это число надо умножить на ½. Таким образом, полная вероятность вынесения справедливого решения жюри из трех человек равна p ² + p (1 − p ) = p , что совпадает с соответствующей вероятностью для жюри из одного человека.
4. Решение задачи об испытаниях до первого успеха
Кажется ясным, что ответ должен быть 6. Чтобы это проверить, обозначим через p вероятность появления шестерки. Тогда вероятности первого успеха при данном испытании равны ( q = 1 − p ):
| Испытания | 1 | 2 | 3... |
| Вероятность первого успеха | p | pq | pq² ... |
Сумма вероятностей равна
p + pq + pq ² + ... = p (1 + q + q ² + ...) = p /(1 − q ) = p / p = 1.
Среднее число испытаний m до первого успеха по определению равно
m = p + 2 pq + 3 pq ² + 4 pq ³ + ...
Для нахождения суммы такого ряда применим обычный прием суммирования геометрических рядов
qm = pq + 2 pq ² + 3 pq ³ + ...
Вычитая второе выражение из первого, находим
m − qm = p + pq + pq ² + ...
или
m (1 − q ) = 1, mp = 1, m = 1/ p .
В нашем примере p = 1/6, так что m = 6.
Предыдущие вычисления были проведены подробно, так как геометрическое распределение часто встречается в этой книге. Красивый способ решения этой задачи дается следующим рассуждением: если первое испытание закончилось неудачей, то условное среднее число испытаний равно 1 + m , а если первое испытание закончилось успехом, то условное среднее число испытаний равно 1. Поэтому
Читать дальшеИнтервал:
Закладка:










