Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями
- Название:Пятьдесят занимательных вероятностных задач с решениями
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями краткое содержание
Книга обращена к широкому кругу читателей: ученикам старших классов, педагогам, студентам.
Пятьдесят занимательных вероятностных задач с решениями - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Из таблиц [6] См. Ф. Мостеллер, Р. Рурке, Дж. Томас. Вероятность, «Мир», 1969, стр. 397.
находим:
lg 12! = 8.68034, lg 51! = 66.19065,
lg 39! = 46.30959, lg (12!·39!) = 54.98993,
lg (12!·39!) = 54.98993, lg(12!·39!/51!) = 11.20072,
12!·39!/51! = 1.588·10 −11.
При вычислениях такого рода точный ответ часто приводит в замешательство. Что из того, что в одном из 160 миллиардов случаев имеется возможность получить «масть»? Сколь часто должны мы были бы слышать о таком событии? Явно завышая числа, предположим, что в США в бридж играют 10 миллионов, и что каждый игрок играет 10 раз всякий день в году. Это дает 36½ миллиардов игр в год, так что исключительную сдачу можно ожидать один раз в 4 года (причем о некоторых из них заведомо не будет объявлено публично). Даже в два раза большее количество игроков, которые играют к тому же в два раза чаще, привело бы лишь к одной такой сдаче в течение года.
Чем можно объяснить значительную большую частоту сообщений о появлении «масти»? Многими причинами, среди которых следует назвать склеивание карт и плохое тасование. (Нашумевший случай «масти», действительно имевший место, произошел при первой раздаче новой колоды.)
Несомненно также, что некоторые репортеры стали жертвами шуток и мистификаций. Если вы подстроили своей бабушке «масть» в день ее рождения и хотите потом сознаться в этом, то вы, наверное, все же промолчите, после того как об этом исключительном событии будут оповещены все родственники, друзья и. репортеры. С другой стороны, ввиду внимания к столь редким явлениям, кажется неправдоподобным, чтобы такую комбинацию подстраивали шулера.
Несколько другим путем решения этой задачи является применение биномиальных коэффициентов, которые равны числу различных способов размещений a элементов одного рода и b элементов другого в строку. Например, 3 буквы a и 2 буквы b могут быть записаны подряд 10 различными способами, что нетрудно проверить на пальцах, начиная с aaabb и кончая bbaaa . Биномиальный коэффициент записывается в этом случае как  и равен числу способов различного упорядочения пяти предметов, два из которых одного рода и три другого. С помощью факториалов этот коэффициент перепишется в виде
и равен числу способов различного упорядочения пяти предметов, два из которых одного рода и три другого. С помощью факториалов этот коэффициент перепишется в виде
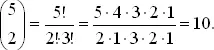
В более общей ситуации, когда имеется n предметов, из которых a одного рода, и n − a — другого, число способов их упорядочения дается формулой
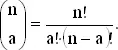
В нашей задаче число способов выбрать 13 карт из полной колоды равно
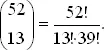
Тринадцать пик можно получить
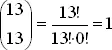
способом, так как 0! = 1. Учитывая, что имеется четыре масти, получим окончательно вероятность в виде 4×13!·39!/52!, как уже было установлено ранее.
Биномиальные коэффициенты обсуждаются в в цитированной выше книге Мостеллера, Рурке и Томаса «Вероятность» на стр. 33–39.
9. «Крэпс»
Эта игра, как мы скоро увидим, удивительно близка к безобидной, хотя все же и невыгодна для игрока.
Подсчитаем сначала вероятности для полного числа очков на двух костях. Сделаем кости различимыми, окрасив их, скажем, в красный и зеленый цвета. Тогда подбрасывание 2-х костей имеет 6×6 = 36 равновероятных исходов, которые приведены ниже в таблице.
| Зеленая кость | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| Красная кость | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
В клетках указана соответствующая сумма очков.
Простым подсчетом мы находим распределение вероятностей суммы очков при одновременном подбрасывании двух костей.
| Сумма | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| P (суммы) | 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 |
Здесь P обозначает вероятность появления соответствующей суммы очков.
Вероятность выигрыша после первого бросания равна
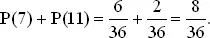
Вероятность проигрыша после первого бросания равна
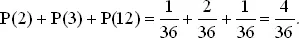
Для дальнейших бросаний нам надо знать вероятность того, что выпадет «пойнт». Так как нам важны лишь очки, отвечающие «пойнт» или 7, то можно вычислять условные вероятности выбросить «пойнт» при условии, что при первом бросании появился «пойнт». Иногда этот метод называется методом «приведенного выборочного пространства», так как хотя в принципе возможны все варианты от 2 до 12 очков, мы рассматриваем лишь «пойнт» и 7.
Например, если выпало 4 очка, то существует 3 возможных способа их появления и 6 способов для появления 7 очков. Таким образом, условная вероятность выбросить «пойнт» равна 3/(3 + 6) = 3/9.
Аналогично условные вероятности других очков «пойнт» равны
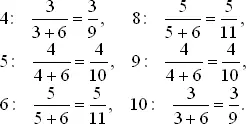
Для определения безусловной вероятности выигрыша при данной сумме «пойнт» надо умножить вероятность получения «пойнт» при первом бросании на условную вероятность выигрыша. Суммируя эти величины, находим вероятность выигрыша для суммы «пойнт»:
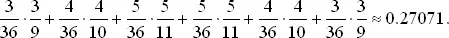
Прибавляя к этому значению вероятность выигрыша при первом бросании 8/36 ≈ 0.22222, видим, что полная вероятность выигрыша игрока равна 0.49293. Его средний ущерб равен 0.50707 − 0.49293 = 0.01414 или 1.41 %. Автор считает, что это наиболее справедливая игра без стратегии, которая практикуется в игорных домах.
Некоторым читателем может показаться слишком искусственным подход, связанный с условными вероятностями. Мы дадим и другой метод, связанный с суммированием бесконечных рядов.
Пусть P обозначает вероятность получить «пойнт», а R — вероятность появления суммы очков, при которой игра продолжается ( R = 1 − P − 1/6). Здесь 1/6, конечно, имеет смысл вероятности появления 7. Игрок выигрывает при r + 1 бросании, если игра продолжалась r шагов, и при r + 1 шаге появился «пойнт». Вероятность этого события равна R rP , r = 0, 1, 2, ... Суммируя по r , получаем
Читать дальшеИнтервал:
Закладка:










