Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями
- Название:Пятьдесят занимательных вероятностных задач с решениями
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями краткое содержание
Книга обращена к широкому кругу читателей: ученикам старших классов, педагогам, студентам.
Пятьдесят занимательных вероятностных задач с решениями - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
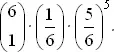
Аналогично, вероятность появления ровно x шестерок при бросании шести костей равна
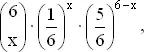 x = 0, 1, 2, 3, 4, 5, 6.
x = 0, 1, 2, 3, 4, 5, 6.
Вообще вероятность появления x шестерок при n бросаниях равна
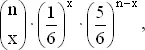 x = 0, 1, 2, 3, ..., n .
x = 0, 1, 2, 3, ..., n .
Эта формула задает вероятности, отвечающие так называемому биномиальному закону.
Вероятность появления хотя бы одной шестерки при шести бросаниях равна
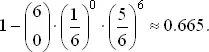
При бросании 6 n костей вероятность появления не менее n шестерок равняется
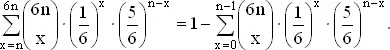
Ньютону пришлось самому вычислять эти вероятности. Мы же можем прибегнуть к помощи таблиц (см., например, Ф. Мостеллер, Р. Рурке, Дж. Томас, Вероятность, стр. 325 и 398). Наша табличка дает вероятности получения числа шестерок, не меньшего, чем математическое ожидание числа их появления, в 6 n бросаниях.
| 6 n | 6 | 12 | 18 | 24 | 30 | 96 | 600 | 900 |
| n | 1 | 2 | 3 | 4 | 5 | 16 | 100 | 150 |
| P | 0.665 | 0.619 | 0.597 | 0.584 | 0.576 | 0.542 | 0.517 | 0.514 |
Итак, Пепайсу следовало предпочитать пари с шестью бросаниями пари с бо́льшим числом бросаний.
Биномиальное распределение рассматривается в уже цитированной книге «Вероятность», гл. VI.
20. Решение задачи о трехсторонней дуэли
У дуэлянта A мало оснований для оптимизма по поводу настоящей дуэли. Если он стреляет первым, то при попадании в C наверняка B попадет в него, поэтому A не должен стрелять в C . Если же A выстрелит в B и промахнется, то B , наверное, выведет из строя более опасного C первым и A сможет стрелять в B с вероятностью попадания 0.3. Если же A промахнется, то его песенка спета. С другой стороны, предположим, что A попадет в B . Тогда C и A будут перестреливаться до первого попадания. Шансы выигрыша A равны
(0.5)·(0.3) + (0.5)²·(0.7)·(0.3) + (0.5)³·(0.7)²·(0.3) + ...
Каждое слагаемое отвечает последовательности промахов C и A , заканчивающихся успехом A . Суммируя геометрический ряд, получаем
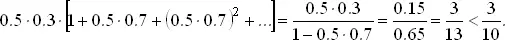
Таким образом, попасть в B и затем покончить с C — стратегия, дающая для A меньшую вероятность выигрыша, чем пропуск первого выстрела. Поэтому A должен стрелять в воздух, а затем стараться попасть в B .
Обсуждая эту задачу с Т. Лерером, я спросил его, благородно ли это решение с точки зрения кодекса о дуэлях. Лерер возразил, что подобный кодекс для дуэлей с тремя участниками не разработан, так что мы с полным основанием можем простить A преднамеренный промах.
21. Решение задачи о выборке с возвращением
Если первый вытянутый шар — красный, то неважно, из какой урны он вынут, так как теперь в этой урне будет поровну красных и черных шаров и второй шар не даст оснований для решения. Поэтому, если сначала вытянут красный шар, следует вернуть его в урну перед вторым извлечением. Если же вынут черный шар, то лучше не возвращать его в урну.
При такой стратегии вероятность правильного ответа равна:
| Урна A | Урна B | Решение | |
| Оба красные | 1/2·2/3·2/3 | 1/2·101/201·101/201 ≈ 1/8 | Урна A |
| Красный, черный | 1/2·2/3·1/3 | 1/2·101/201·100/201 ≈ 1/8 | Урна B |
| Черный, красный | 1/2·1/3·1 | 1/2·100/201·101/201 ≈ 1/8 | Урна A |
| Оба черные | 1/2·1/3·0 | 1/2·100/201·99/200 ≈ 1/8 | Урна B |
Полная вероятность правильного решения приближенно равна (заменяя 100/201 на 1/2 и т. д.):
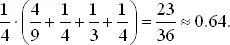
Если вытягивать оба шара без возвращения, то вероятность угадать приблизительно равна 5/8, а при возвращении 21.5/36 (0.625 < 0.597).
22. Решение задачи о выборах
При a = 3 и b = 2 всеми возможными равновероятными последовательностями извлечения бюллетеней являются следующие:
АААВВ *ААВВА *АВВАА
*АВАВА *ВАВАА *ВААВА
*ВВААА ААВАВ *АВААВ
*ВАААВ ,
где звездочкой отмечены комбинации, в которых имеет место равновесное положение. Таким образом, в нашем случае искомая вероятность равна 8/10.
Перейдем теперь к общей ситуации произвольных a и b . Рассмотрим сначала те последовательности, в которых первое равновесное положение достигается в случае, когда подсчитаны 2 n бюллетеней, n ≤ b . Каждой последовательности, в которой A лидирует до первого ничейного результата, соответствует единственная последовательность, в которой лидирует B . Так, при n = 4 последовательности
ААВАВАВВ
с лидером A отвечает последовательность
ВВАВАВАА
в которой лидирует B . Эта последовательность получается из первой заменой A на B и B на A .
Итак, число последовательностей, в которых A лидирует до первой ничьей, равно числу последовательностей с лидером B . Задача сводится, таким образом, к вычислению вероятности равновесного положения, до которого лидирует B .
Так как за A подано большее количество голосов, то рано или поздно A становится лидером. Если первый бюллетень подан за B , то ничья неизбежна. Единственной возможностью ничьей с B , лидирующим в начале, является случай, когда первый бюллетень подан за B . Вероятность того, что это так, равна b /( a + b ). Но это же значение равно вероятности ничьей с лидирующим в начале A , и, таким образом, вероятность ничейного положения равна
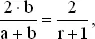
где r = a / b . Заметим, что если a много больше, чем b , т. е. когда r велико, вероятность ничьей мала (что интуитивно вполне понятно). Формула верна также и при b = a , так как в этом случае вероятность ничьей равна единице.
23. Решение задачи о ничьих при бросании монеты
Ниже мы обобщим метод решения задачи 22 и покажем, что вероятность отсутствия ничейного результата (при N четном и N нечетном) равна
Читать дальшеИнтервал:
Закладка:










