Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями
- Название:Пятьдесят занимательных вероятностных задач с решениями
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями краткое содержание
Книга обращена к широкому кругу читателей: ученикам старших классов, педагогам, студентам.
Пятьдесят занимательных вероятностных задач с решениями - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Сумма выражений (A) и (B) дает нам удвоенную вероятность четного числа кексов, так как члены с нечетными степенями m войдут в сумму с нулевыми коэффициентами, а члены с четными степенями — с коэффициентом 2. Следовательно, деля на 2, получим вероятность четного числа покупок (1 + e −2 m )/2. При m = 20 этот результат весьма близок к 0.5, так как число e −40мало́. С другой стороны, если булочник продает в среднем один специальный торт ко дню рождения за одну поездку, то вероятность того, что будет продано четное число таких тортов, равняется приблизительно 0.568.
31. Решение задачи о парных днях рождения
В задачах такого рода предполагается обычно, что 29 февраля не может быть днем рождения, и что всем остальным дням в году отвечает одинаковая вероятность.
Решим несколько более общую задачу. Пусть N обозначает число равновероятных дней, r — число людей. Вычислим вероятность того, что все эти люди родились в разные дни. Тем самым мы найдем и вероятность того, что хотя бы два человека родились в один и тот же день.
Для первого человека имеется N возможных дней, для второго — ( N − 1), не совпадающих с днем рождения первого, для третьего — ( N − 2), отличных от дней рождения первых двух и т. д., для r -го человека существует N − r + 1 возможностей. Общее число вариантов, при которых нет одинаковых дней рождения, равно
N ·( N − 1)·...·( N − r + 1) ( r сомножителей). (1)
Для определения интересующей нас вероятности надо найти еще общее число всевозможных расстановок дней рождения. Для каждого человека существует ровно N возможных дней, и общее число различных распределений дней рождения r людей равно
N r . (2)
Так как, согласно предположению, все дни равновероятны, то искомая вероятность равна отношению (1) и (2). Таким образом, вероятность того, что имеются по крайней мере два одинаковых дня рождения, равна
P r = 1 − N ·( N − 1)·...·( N − r + 1)/ N r . (3)
Точное вычисление значения (3) потребовало бы при больших значениях N таких, как 365, значительного числа выкладок, чего в нашем случае можно избежать за счет использования таблицы логарифмов, представляя искомую вероятность в виде N ! / ( N − 2)!· N r . Имеем
| lg(365!) = 778.399975, | lg(365) = 2.56229286 |
| r = 20, | lg(345!) = 727.38410, |
| r = 21, | lg(344!) = 724.84628, |
| r = 22, | lg(343!) = 722.30972, |
| r = 23, | lg(342!) = 719.77442, |
| r = 24, | lg(341!) = 717,24040, |
| r = 25, | lg(340!) = 714.70764. |
Небольшая работа с таблицами показывает, что при r = 23 вероятность по крайней мере одного совпадения дня рождений равна 0.5073, а при r = 22 эта вероятность равна 0.4757. Таким образом, r = 23 — наименьшее целое число, при котором имеет смысл заключать равноправное пари. Для большинства кажется удивительным, что это число довольно мало́, так как интуитивно ожидаемым ответом кажется 365/2. Мы обсудим это явление в следующей задаче, а пока заметим вот что:
Во-первых, следующая таблица дает значения вероятности парных дней рождения для различных значений R :
| R | 5 | 10 | 20 | 23 | 30 | 40 | 60 |
| P R | 0.027 | 0.117 | 0.411 | 0.507 | 0.706 | 0.891 | 0.994 |
Во-вторых, вспомним, что
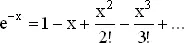
Если x достаточно мало́, то члены порядка, большего, чем x , дают в сумму пренебрежимо малый вклад, и e −x приближенно равно 1 − x , или 1 − x можно при малых x заменить на e −x . Заметим, что
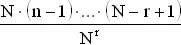
является произведением множителей вида ( N − k )/ N , где k много меньше N . Эти множители могут быть записаны в виде 1 − k / N , где 0 ≤ k ≤ r . Поэтому

Для исследования этой асимптотической формулы положим r = 23 и получим что-то около 0.500 вместо 0.507, или, положив r ·( r − 1)/2·365 равным −lg(0.5) ≈ 0.693, найдем отсюда r .
В-третьих, предположим, что задача модифицирована таким образом: найти вероятность того, что хотя бы два дня рождения совпадают или приходятся на два дня, следующих один за другим (1 января следует за 31 декабря). Решение такой задачи предоставляется читателю.
32. Решение задачи «В поисках парных дней рождения»
Автор считает, что большинство людей имеет в виду именно эту задачу, когда им предлагают задачу 31 о парных днях рождения. Мысль о дне рождения, совпадающем с вашим, и вызывает удивление при ответе r = 23 в задаче о парных днях рождения. В настоящих условиях вам совсем не важно, совпадают ли дни рождения других людей, если только они не совпадают с вашим. Чаще всего считают, что ответ в этой задаче равен половине от 365 или 183. Из-за смешения двух проблем ответ r = 23 кажется тогда неправдоподобно маленьким.
Но и в настоящей задаче интуитивный ответ 183 оказывается неправильным. Дело в том, что выборка дней рождения производится с возвращением. Если первый из опрошенных родился 4-го июля, то ничто не мешает и последующим иметь тот же день рождения. Вероятность того, что опрошенный человек родился не в один день с вами, равна ( N − 1)/ N , где N = 365 — число дней в году. При опросе n людей вероятность того, что все они произошли на свет не в ваш день рождения, равна [( N − 1)/ N ] n , и вероятность того, что хотя бы у одного день рождения тот же самый, что и ваш, равна
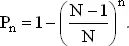 (4)
(4)
Нас интересует наименьшее значение n , для которого P n не меньше 1/2. Логарифм 364 равен 2.56110, а 1/2 равен −0.30103.
Если мы перейдем к логарифмам, то обнаружим, что искомое значение n равно 253, что довольно значительно отличается от 183.
Можно поступить и иначе, использовав опять аппроксимацию
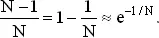
Тогда
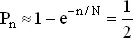
и
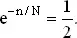
Логарифмируя, получаем n / N ≈ 0.693, n ≈ 0.693N. Для N = 365 получаем n = 253.
Эта задача легче предыдущей, и обсуждение связи между их ответами представляется поучительным.
33. Решение задачи о соотношении между разными задачами о парных днях рождения
Интервал:
Закладка:










