Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями

n = p ·1 + q (1 + m ) = 1 + qm и m = 1/ p .

Когда мы бросаем монету на стол, то некоторые области положения центра тяжести монеты вероятнее других, но если квадрат достаточно мал, можно считать, что распределение вероятностей равномерно. Это означает, что вероятность попадания центра в какую-либо область квадрата пропорциональна площади этой области; она равна площади области, деленной на площадь квадрата. Так как радиус монеты равен 3/8 дюйма, то для выигрыша игрока центр не должен находиться ближе, чем 3/8 дюйма от сторон квадрата (рис. 3). Этому ограничению отвечает квадрат со стороной 1/4 дюйма, внутри которого должен лежать центр монеты. Так как вероятности пропорциональны площадям, то вероятность выигрыша равна (1/4)² = 1/16. Разумеется, монета вообще может не попасть на стол, и вероятность вы выигрыша на самом деле еще меньше. Квадраты также могут быть уменьшены за счет утолщения разделяющих линий. Если эти линии имеют толщину и 1/16 дюйма, то выигрышной области соответствует вероятность (3/16)² = 9/236, или меньше 1/28.

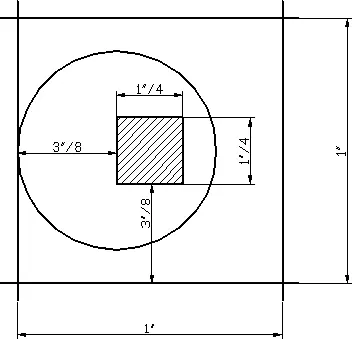
Рис. 3. Заштрихованная область отвечает случаю, когда игрок выигрывает.

Подсчитаем ущерб, возникающий в следующих случаях: (а) номера всех трех костей различны, (б) имеются ровно два одинаковых номера и (в) все три номера одинаковы. Предположим для простоты, что на каждый номер поставлена единичная ставка. Пусть для начала выпало три различных номера, скажем, 1, 2 и 3. Тогда игорный дом получает три единичные ставки на выигравших номерах 4, 5, 6 и расплачивается ими за три проигравших номера: 1, 2, 3. В этом случае нет ни выигравших, ни проигравших. Ясно, что так будет всегда, когда выпадают три различных номера.

Предположим теперь, что после подбрасывания костей выпало ровно два одинаковых номера, например, 1, 1 и 2. В этом случае игорный дом может использовать ставки, поставленные на номера 3 и 4, как расплату с номером 1, а ставку с номера 5 уплатить номеру 2. Деньги же, поставленные на нономер 6, таким образом, остаются игорному дому. Итак, игорный дом в этом случае выигрывает одну ставку, а игрок ее теряет, так что при единичной ставке ущерб последнего равен 1/6.

Наконец, пусть на всех костях выпало одно и то же число, скажем, 1, 1, 1. Тогда игорный дом выплачивает сумму, равную утроенной ставке, из денег, поставленных на номера 2, 3, 4, оставляя себе ставки, соответствующие номерам 5 и 6. В этом случае потеря игрока, рискующего одной ставкой, равна 2/6. Любопытно заметить, что в среднем игроки теряют больше всего в случаях двух и трехкратной выплаты.

Для определения среднего ущерба, соответствующего единичной ставке, нужно найти вероятности рассмотренных случаев. Пусть игральные кости различаются по цвету, скажем, красная, зеленая и синяя. Они могут выпасть 6·6·6 = 216 способами.

Скольким из этих способов отвечают три различных номера? Если для красной кости имеется 6 вариантов, то для зеленой уже только 5, так как номер, выпавший на красной кости, не должен повториться. Зеленая кость может выпасть по аналогичным соображениям лишь одной из четырех граней, отличных от предыдущих. Итак, всего существует 6·5·4 = 120 возможных вариантов.

Оставим на время второй случай и перейдем к рассмотрению третьего — когда выпадает три одинаковых номера. Число таких вариантов равно 6, так как красная кость может выпасть шестью различными способами, зеленая же и синяя только одним, а именно тем, которым выпала красная.

Это означает, что существует 216 − 126 = 90 комбинаций, при которых выпадает ровно два одинаковых номера. В этом, впрочем, можно убедиться и непосредственно. Возможны следующие сочетания костей с одинаковыми номерами: красно-зеленая, красно-синяя и зелено-синяя. Для нахождения общего числа комбинаций определим число возможных вариантов, скажем, для сочетания красно-зеленая, и умножим его на три. Красная кость может выпасть шестью способами, зеленая — только одним и синяя — пятью, т. е. всего существует 30 таких вариантов. Окончательный результат 3·30 = 90 совпадает с почученным ранее.

Средний ущерб получается суммированием произведений вероятностей отдельных случаев на ущерб, им соответствующий:

120/216 · 0 + 90/216 · 1/6 + 6/216 · 2/6 = 17/216 ≈ 0.079 [5] Знак ≈ означает «приближенно равно». .

Итак, в среднем игрок теряет 8 % своей ставки. Учитывая, что игра продолжается около 30 секунд, а по государственным облигациям выплачивается менее 4 % доли прибыли за год, такую игру можно назвать чудовищно несправедливой.

Проведенные расчеты верны лишь для правильных костей. Иногда вместо костей употребляется крутящееся колесо со стрелкой, которое после остановки показывает на участок окружности, отвечающий определенной комбинации из трех цифр. При этом относительные длины этих участков плохо согласуются с вероятностями появления соответствующих комбинаций при подбрасывании костей. Наблюдения показывают, что для таких колес двух- и трехкратные выплаты встречаются чаще и, значит, средний ущерб еще больше.

Если Браун выиграет хоть один раз за 36 игр, он не потерпит убытка. Вероятность проиграть все 36 раз равна

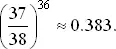
Математическое ожидание выигрыша в одной игре есть

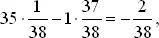
а в 36 играх:

При игре против благожелательного друга математическое ожидание выигрыша Брауна равно

20·0.617 − 20·0.383 = 4.68.

В итоге Браун в среднем получит 4.68 − 1.89 = 2.79 доллара за 36 игр и будет в выигрыше. Возможно, доброжелательный друг будет сам переубежден. Разумеется, если Браун проиграет все 36 игр, то потеряет 56 долларов, что весьма неприятно.

Эта вероятность ничтожно мала. Так как колода хорошо перетасована, можно считать, что 13 карт сняты сверху. Для получения 13 карт одной масти нужно, вытащив сначала любую из 52 карт, извлечь затем все карты той же масти (которых всего 13 штук). Итак, число способов получения «масти» равно

52·12·11·10·9·8·7·6·5·4·3·2·1 = 52·12!

Общее же число способов извлечения 13 карт из 52 равно

52·51·50·49·48·47·46·45·44·43·42·41·40 = 52!/39!

Искомая вероятность равна 52·12!/(52!/36!) = 12!·39!/51! Обратная величина может трактоваться как среднее число игр до появления «масти».