Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями

(а). Урна содержит 10 черных и 10 белых шаров, отличающихся лишь цветом. Один шар вытаскивается наружу, и если его цвет совпадает с выбранным вами, то вы получаете 10 долларов, в ином случае — ничего. Сообщите максимальный взнос, который вы готовы сделать для участия в игре. Игра проводится лишь один раз.

(б). У вашего друга имеется много белых и черных шаров, и он заполняет ими урну по своему усмотрению. Вы выбираете «черное» или «белое», после чего из урны наудачу вытягиваете шар. Какую максимальную сумму вы готовы заплатить за участие в игре? Игра проводится только один раз.

О. Хелмер и Дж. Уильяме обратили внимание автора на ряд задач, которые они называют «задачами без структуры», но которые все же имеют вероятностный характер, хотя и не в обычном смысле.

Двум незнакомым людям предлагается загадать произвольное натуральное число, причем если они оба называют одно и то же число, то получают премию. Какое бы число загадали вы?

Двое незнакомых людей, договорившись о том, как узнать друг друга, должны встретиться в определенный день и час в Нью-Йорке, городе, которого они оба не знают. Однако они забыли назначить место встречи. Куда им следует направиться, если они все же попытаются встретиться? [2] Для решения задачи нужно, конечно, знакомство с наиболее часто посещаемыми местами Нью-Йорка. См. обсуждение задачи (прим. перев.) .

Три узника, A , B и C , одинаково хорошего поведения ходатайствовали об освобождении на поруки. Администрация решила освободить двух из трех, что стало известно узникам, которые, однако, не знают, кто именно эти двое. У заключенного A в охране есть друг, который знает, кого отпустят на свободу, но A считает неэтичным осведомиться у охранника, будет ли он, A , освобожден. Все же A хочет спросить об имени одного узника, отличного от самого A , который будет отпущен на свободу. Прежде чем спрашивать, он оценивает вероятность своего освобождения как 2/3. A думает, что если охранник скажет « B будет освобожден», то его шансы уменьшатся до ½, так как в этом случае будут освобождены либо A и B , либо B и C . Однако A ошибается в своих расчетах. Объясните это.

Купоны в коробках занумерованы цифрами от 1 до 5, и для того, чтобы выиграть, надо набрать полный комплект из пяти купонов с разными номерами. Если из коробки вынимается один купон, то сколько коробок в среднем надо испытать, чтобы получить полный комплект?

Восемь юношей и семь девушек независимо приобрели по одному билету в одном и том же театральном ряду, насчитывающем 15 мест. Какое среднее число смежных мест занимают в этом ряду пары?

В теннисном турнире участвуют 8 игроков. Номер, вытаскиваемый игроком наудачу, определяет его положение в турнирной лестнице (рис. 1).

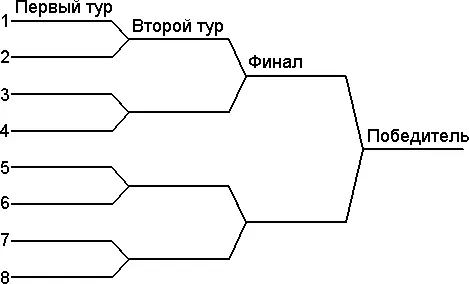
Рис. 1. Турнирная лестница для 8 участников.

Предположим, что лучший игрок всегда побеждает второго по мастерству, а тот в свою очередь побеждает всех остальных. Проигрывающий в финале занимает второе место. Какова вероятность того, что это место займет второй по мастерству игрок?

(а). Король Артур проводит рыцарский турнир, в котором, так же как и в теннисе, порядок состязания определяется жребием (см. задачу 16). Среди восьми рыцарей, одинаково искусных в ратном деле, два близнеца. Какова вероятность того, что они встретятся в поединке?

(б). Каков ответ в случае 2 n рыцарей?

При бросании 100 монет какова вероятность выпадения ровно 50 гербов?

С. Пепайс предложил Исааку Ньютону следующую задачу: Какое из событий более вероятно: (а) появление по крайней мере одной шестерки при подбрасывании 6 костей, (б) появление хотя бы двух при подбрасывании 12 костей и (в) появление не менее трех шестерок при бросании 18 костей?

A , B и C сходятся для трехсторонней дуэли. Известно, что для A вероятность попасть в цель равна 0.3, для C — 0.5, а B стреляет без промаха. Дуэлянты могут стрелять в любого противника по выбору. Первым стреляет A , затем B , дальше C и т. д. в циклическом порядке (раненый выбывает из дуэли), пока лишь один человек не останется невредимым. Какой должна быть стратегия A ?

Две урны содержат красные и черные шары, не различимые на ощупь. Урна A содержит 2 красных и 1 черный шар, урна B — 101 красный и 100 черных шаров. Наудачу выбирается одна из урн, и вы получаете награду, если правильно называете урну после вытаскивания двух шаров из нее. После вытаскивания первого шара и определения его цвета вы решаете, вернуть ли в урну этот шар перед вторым вытаскиванием. Какой должна быть ваша стратегия?

После выборов, в которых участвуют два кандидата, A и B , за них поступило a и b ( a > b ) бюллетеней соответственно, скажем, 3 и 2. Если подсчет голосов производится последовательным извлечением бюллетеней из урны, то какова вероятность того, что хотя бы один раз число вынутых бюллетеней, поданных за A и B , было одинаково?

Игроки A и B в орлянку играют N раз. После первого бросания каковы шансы на то, что в течение всей игры их выигрыши не совпадут?

Мэрвин кончает работу в случайное время между 15 и 17 часами. Его мать и его невеста живут в противоположных частях города. Мэрвин садится в первый подошедший к платформе поезд, идущий в любом направлении, и обедает с той из дам, к которой приедет. Мать Мэрвина жалуется на то, что он редко у нее бывает, но юноша утверждает, что его шансы обедать с ней и с невестой равны. Мэрвин обедал с матерью дважды в течение 20 рабочих дней. Объясните это явление.