Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями
- Название:Пятьдесят занимательных вероятностных задач с решениями
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями краткое содержание
Книга обращена к широкому кругу читателей: ученикам старших классов, педагогам, студентам.
Пятьдесят занимательных вероятностных задач с решениями - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Более формально, с каждой парой карт может быть связана случайная величина X i , которая равна 1 в случае, если карты одинаковы, и 0, если карты различны. Имеем
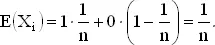
Наконец, общее число совпадений равно ∑ X i и в силу уже упоминавшейся теоремы
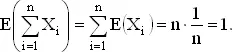
46. Решение задачи о вероятностях совпадений
Эта задача родственна задаче 28, в которой мы впервые встретились с законом Пуассона. Однако в задаче о фальшивомонетчике в силу независимости испытаний появление фальшивой монеты было равновероятно на каждом шагу, в настоящей же задаче совпадения для каждой пары не являются независимыми. Например, если n − 1 пар совпали, то необходимо совпадет и n -я пара, так что эти события действительно зависимы. Тем не менее при больших значениях n степень зависимости невелика, так что, казалось бы, вероятность r совпадений в этой задаче должна быть близка к вероятности обнаружения фальшивых монет, задаваемой распределением Пуассона. В конце мы сравним решение такой задачи с ответом, получаемым из закона Пуассона со средним 1.
При решении таких задач оказывается полезным рассмотрение частных случаев, отвечающих небольшим значениям n . При n = 1 совпадение неизбежно. При n = 2 вероятность отсутствия совпадения равна 1/2, вероятность двух совпадений также равняется 1/2. При n = 3 занумеруем карты цифрами 1, 2 и 3 и запишем в таблицу 6 возможных перестановок для верхней колоды при фиксированном порядке (1, 2 ,3) нижней.
| Нижняя колода | 1 | 2 | 3 | Число совпадений |
| Перестановки верхней колоды | 1 | 2 | 3 | 3 |
| 1 | 3 | 2 | 1 | |
| 2 | 1 | 3 | 1 | |
| 2 | 3 | 1 | 0 | |
| 3 | 1 | 2 | 0 | |
| 3 | 2 | 1 | 1 |
Отсюда получаем
| Число совпадений | 0 | 1 | 2 | 3 |
| Вероятность | 2/6 | 3/6 | 0/6 | 1/6 |
Приведем также соответствующую таблицу для n = 4. Легко заметить, что вероятность того, что произойдет n совпадений, равна 1/ n !, поскольку только одной из n ! перестановок отвечает n совпадений.
| Число совпадений | 0 | 1 | 2 | 3 | 4 |
| n = 1, вероятность | 0 | 1 | |||
| n = 2, вероятность | 1/2 | 0 | 1/2 | ||
| n = 3, вероятность | 2/6 | 3/6 | 0 | 1/6 | |
| n = 4, вероятность | 9/24 | 8/24 | 6/24 | 0 | 1/24 |
Отметим, что математическое ожидание каждого распределения равно 1, как указано в предыдущей задаче.
Пусть P ( r / n ) обозначает вероятность ровно r совпадений при распределении n объектов. Эти r совпадений могут быть получены за счет совпадения r фиксированных объектов и несовпадения остальных. Так, например, вероятность того, что совпадают именно r первых объектов, равна
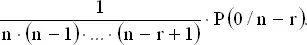
Число различных выборов r объектов из n равно 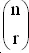 так что
так что
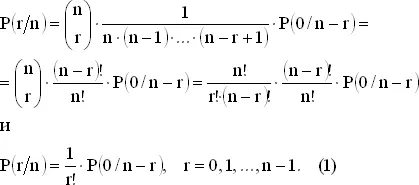
При r = n , как мы знаем, P ( n / n ) = 1/ n !, и мы можем положить P (0/0) = 1.
Проверим справедливость соотношения (1) при n = 4, г = 2. Согласно (1)
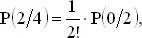
а из нашей таблицы видно, что
P (2/4) = 6/24,
P (0/2) = 1/2
и 6/24 = 1/4, что подтверждает (1) в этом частном случае.
Мы знаем также, что сумма вероятностей по всем возможным числам совпадений при заданном значении n равна 1, т. е.
P (0/ n ) + P (1/ n ) + ... + P ( n − 1/ n ) + P ( n / n ) = 1.
Используя (1), запишем это соотношение как
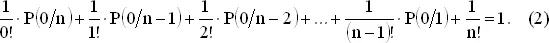
Так как P ( n / n ) = 1/ n !, то отсюда можно последовательно находить значения P (0/ n ).
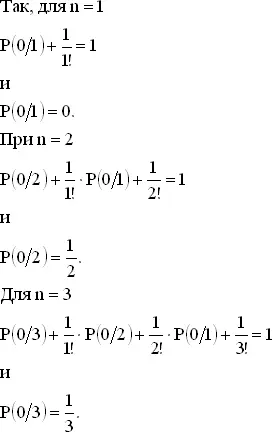
Итак, мы можем найти в принципе значение P (0/ n ) при любом n , но не располагаем общей формулой для вычисления P (0/ n ). Как и в некоторых других задачах, здесь помогает вычисление последовательных разностей. Подсчитаем P (0/ n ) − P (0/ n − 1) для различных значений n . Имеем
P (0/1) − P (0/0) = 0 − 1 = −1 = −1/1!,
P (0/2) − P (0/1) = 1/2 − 0 = 1/2 = 1/2!,
P (0/3) − P (0/2) = 2/6 − 1/2 = −1/6 = −1/3!,
P (0/4) − P (0/3) = 9/24 − 2/6 = 1/24 = 1/4!.
Эти выкладки наводят на мысль о том, что искомые разности имеют вид (-l) r / r !, т. е.
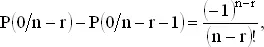
Суммируя эти разности, получаем
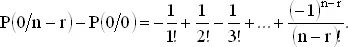
Записывая P (0/0) в виде 1/0!, получаем
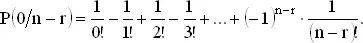 (3)
(3)
Осталось проверить теперь справедливость нашей догадки. Нам надо вычислить
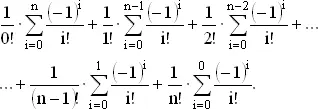 (4)
(4)
Не следует терять хладнокровия. при виде этого зловещего выражения. Ведь сумма в (4) образована слагаемыми вида
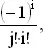
где индекс j отвечает множителю, стоящему перед знаком суммы, а индекс i соответствует отдельным членам этой суммы. Переставим местами слагаемые так, чтобы сумма i + j была постоянной. Так, для i + j = 3 получим
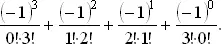
Умножая на 3!, получаем более знакомое выражение
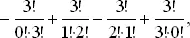
которое с помощью биномиальных коэффициентов может быть записано в виде
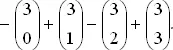
Но эта сумма есть разложение ( x + y )³ при х = −1, y = 1 и, значит, равна нулю, так как (-1 + 1)³ = 0³ = 0. Этот факт имеет место при каждом значении i + j = r , r = 1, 2, ...., n , так что соответствующие суммы равны нулю. Лишь при r = 0 получаем единственный член (-1) 0/(0!·0!) = 1. Следовательно, решение (3) удовлетворяет уравнению (2).
Читать дальшеИнтервал:
Закладка:










