Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями

Да. Пусть A — длина длинного стержня, а B — длина короткого. Можно положить эти стержни рядом и измерить разность длин A − B , а затем приложить их один к другому и измерить сумму длин A + B . Пусть D и S обозначают наблюденные длины A − B и A + B соответственно. Тогда оценка для A есть 1/2( S + D ) и оценка для B есть 1/2( S − D ). Далее, D = A − B + d , S = A + B + s , где d и s — случайные ошибки. Следовательно,

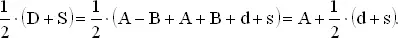
В среднем ошибка 1/2( d + s ) будет нулевой, поскольку d и s имеют средние нуль. Дисперсия оценки A есть дисперсия

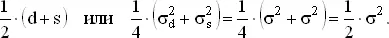
Это значение совпадает со значением для дисперсии среднего двух независимых наблюдении. Таким образом, оба наблюдения внесли полный вклад в измерение A . Точно так же дисперсия оценки B равняется σ²/4. Следовательно, делая два измерения — одно для разности, другое для суммы — мы получаем оценки, точность которых равна точности при четырех рениях, по два на каждый стержень в отдельности.

Для получения столь хороших результатов мы должны как можно точнее соединить концы стержней. Если этого сделать нельзя, то можно считать, что в результаты измерений входит ошибка, связанная с неидеальным совпадением концов стержня. Если эта случайная ошибка имеет штандарт σ√2, то одному измерению суммы или разности отвечает штандарт σ√3/√2, и дисперсия нашей оценки A будет равна

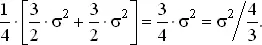
При этих предположениях наша точность будет точно такой же, как и точность при 4/3 независимых измерениях вместо 2, но все же больше точности одного прямого измерения.

Мы можем обосновать предположение о том, что ошибка от неточного совпадения концов имеет штандарт σ/√2, следующим образом. Представим себе s (или d ) как сумму двух независимых ошибок измерения, каждую с дисперсией σ²/2. Тогда сумма слагаемых ошибок имеет дисперсию, которую мы считали

равной σ². Если мы припишем дисперсию σ²/2 и третьему слагаемому, то такая модель будет согласовываться с исходной.

Для того чтобы вопрос задачи имел смысл, предположим, что точка ( b , c ) равномерно распределена на квадрате с центром в начале координат и стороной 2 B (рис. 22). Решим задачу при фиксированном B , а затем устремим B к бесконечности, так что b и c могут принимать любые значения.

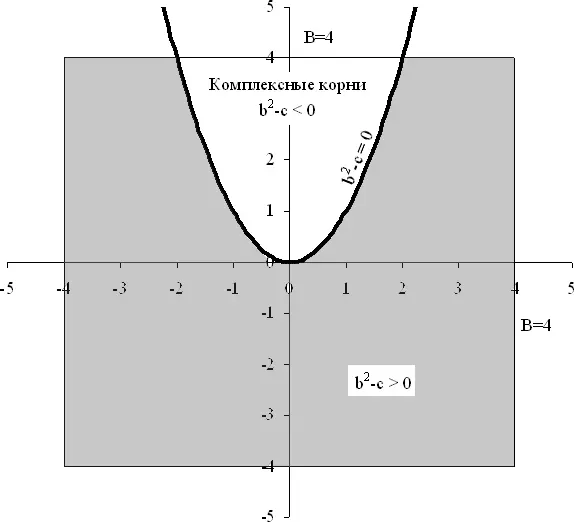
Рис. 22. Серая область отвечает случаю вещественных корней.

Для того чтобы уравнение имело вещественные корни, необходимо и достаточно, чтобы

b ² − c ≥ 0.

На приведенном рисунке изображена парабола b ² = c и показана область, где наше уравнение имеет вещественные корни для B = 4.

Нетрудно подсчитать, что площадь незаштрихованной области равна 4/3∙ B 3/2(при B ≥ 1), а площадь всего квадрата, конечно, равна 4 B ². Следовательно, вероятность того, что корни комплексные, равна 1/3∙√ B . При B = 4 ответ равен 1/6. С ростом B 1/√ B стремится к нулю, так что вероятность того, что корни вещественные, стремится к 1.

Следует заметить, что эта задача отличается от такой же задачи, связанной с уравнением ax ² + 2 bx + c = 0. Конечно, можно разделить на a , но если a , b и c были независимы и равномерно распределены в некотором кубе, то b / a и c / a уже зависимы и распределены неравномерно.

В одномерном случайном блуждании (см. задачу 35 «На краю утеса», последняя часть решения) мы нашли, что вероятность возвращения частицы в начало есть l, если вероятности шагов налево и направо одинаковы. Но положение дел все же весьма деликатно сбалансировано. Если бы одна из вероятностей отличалась от 1/2, то частица удалилась бы в бесконечность. В случае двух измерений можно предположить, что у частицы больше возможностей для ухода в бесконечность. Выясним, так ли это. Мы постараемся найти среднее число возвращений частицы в начало и отсюда определить значение вероятности возвращения частицы. Прежде всего, сколько раз частица вернется в начало? Если P есть вероятность возвращения, то 1 − P = Q есть вероятность того, что возвращения не будет. Тогда вероятность ровно x возвращений есть P xQ , так как после каждого возвращения частицу можно рассматривать как снова выходящую из начала. Если бы P было известно, то среднее число возвращений в начало координат можно было бы найти, суммируя геометрический ряд вида

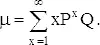
Из задачи 4 об испытаниях до первого успеха видно, что среднее число возвращений есть величина, обратная к вероятности успеха. В упомянутой задаче успех заканчивал серию испытаний, в нашей же задаче серию заканчивает невозвращение в начало, так что среднее число испытаний до первого успеха равно 1/ Q . Следовательно, среднее число успехов равно 1/ Q − 1. Если Q = l, то среднее число успехов равняется 0, и с вероятностью 1 частица будет потеряна и никогда не вернется. С другой стороны, чем меньше Q , тем больше среднее число возвращений. Действительно, каждому значению Q отвечает среднее число возвращений и для каждого среднего числа найдется соответствующее Q . Если среднее число возвращений перед окончательным уходом бесконечно (неограниченно), то Q должно быть равным нулю, а P равным 1. Более формально, P → 1 при µ → ∞. Теперь видно, что для решения задачи о двумерном блуждании мы должны подсчитать значение µ.

Выходя из начала, частица может попасть в него обратно лишь после четного числа шагов. Более того, ее путь может быть представлен как «произведение» двух независимых одномерных случайных блужданий, каждое из которых начинается в начале координат, и одно происходит в вертикальном направлении, а другое — в горизонтальном направлении. После двух шагов горизонтальная компонента x имеет распределение

Вертикальная компонента после двух шагов распределена точно так же, и вероятности их совместного распределения в девяти точках выглядят следующим образом: