Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями
- Название:Пятьдесят занимательных вероятностных задач с решениями
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями краткое содержание
Книга обращена к широкому кругу читателей: ученикам старших классов, педагогам, студентам.
Пятьдесят занимательных вероятностных задач с решениями - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
| Распределение X | |||||
| x | -2 | 0 | 2 | ||
| P ( x ) | 1/4 | 2/4 | 1/4 | ||
| Распределение Y | |||||
| y | P ( y ) | P ( x , y ) | |||
| 2 | 1/4 | 1/16 | 2/16 | 1/16 | |
| 0 | 2/4 | 2/16 | 4/16 | 2/16 | |
| -2 | 1/4 | 1/16 | 2/16 | 1/16 | |
| Совместное распределение X и Y после двух шагов |
Основной факт, на который мы хотим обратить внимание, состоит в том, что вероятность возвращения в начало есть 4/16, и это число ввиду независимости компонент блуждания есть произведение P ( X = 0) на P ( Y = 0). Это допускает следующую интерпретацию. После двух шагов 25 % частиц в среднем вернется в начало. Вклад в среднее число возвращений в начало координат будет тогда равен 4/16·1 + 12/16·0 = 4/16. Вычислим вероятность того, что частица попадет в начало после 2, 4, 6, ... шагов, и, сложив все эти значения, найдем математическое ожидание числа возвращений частицы в начало.
После 2 n шагов, n = 1, 2, ..., вероятность того, что частица вернулась в начало координат, равняется
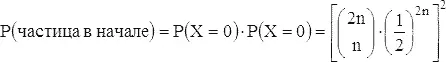
так как для осуществления этого события мы должны иметь равные количества шагов как по вертикали, так и по горизонтали. Строго говоря, надо было бы поставить индексы у X и Y и писать X 2 n и т.д., но это выглядит неприятно и отпугивающе. Просуммируем теперь приближенные выражения для этих вероятностей и найдем математическое ожидание числа возвращений. Для больших значений n можно применить формулу Стирлинга, приведенную в задаче 18, и получить
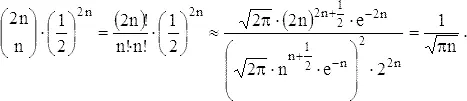
Тогда для больших n имеем
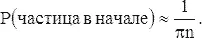
Эти вероятности надо просуммировать по n . Из задачи 14 известно, что 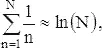 и последнее выражение неограниченно растет с возрастанием N . Найдем вероятность того, что частица вернется в начало после числа шагов, равного 2, 4, 6, 8, , .., 2 n . Каждая из этих вероятностей есть также среднее значение числа случаев, когда частица попадает в начало после ровно 2 n шагов. Чтобы получить общее математическое ожидание числа возвращений частицы в начало, просуммируем эти значения, пользуясь тем фактом, что сумма средних есть среднее суммы. Видим, что среднее число возвращений в начало бесконечно, и вероятность возвращения в начало P = 1. Таким образом, частица не только вернется, но будет возвращаться бесконечное число раз. Более точно, надо сказать, что почти каждая частица возвращается бесконечно часто, так как существуют пути такие, например как постоянное направление на северо-восток, которые позволяют некоторым частицам уходить в бесконечность. Но доля таких частиц равна нулю.
и последнее выражение неограниченно растет с возрастанием N . Найдем вероятность того, что частица вернется в начало после числа шагов, равного 2, 4, 6, 8, , .., 2 n . Каждая из этих вероятностей есть также среднее значение числа случаев, когда частица попадает в начало после ровно 2 n шагов. Чтобы получить общее математическое ожидание числа возвращений частицы в начало, просуммируем эти значения, пользуясь тем фактом, что сумма средних есть среднее суммы. Видим, что среднее число возвращений в начало бесконечно, и вероятность возвращения в начало P = 1. Таким образом, частица не только вернется, но будет возвращаться бесконечное число раз. Более точно, надо сказать, что почти каждая частица возвращается бесконечно часто, так как существуют пути такие, например как постоянное направление на северо-восток, которые позволяют некоторым частицам уходить в бесконечность. Но доля таких частиц равна нулю.
52. Решение вадачи о трехмерном случайном блуждании
Поскольку мы знаем, что в случае одного и двух измерений частица возвращается в начало с вероятностью 1, то не будет ли естественно предположить, что она вернется туда заведомо при любом числе измерений? Казалось бы да, но этот ответ не верен.
В нашем случае положение частицы задается тремя координатами, и вероятность того, что все три координаты равны 0 после 2 n шагов, есть
P (частица в начале) = P ( X =0)·P( Y =0)· P ( Z =0) = 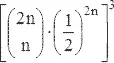 .
.
Применим снова формулу Стирлинга. Мы видим, что на 2 n -м шаге
P (частица в начале) = 1/(π n ) 3/2.
Покажем, что сумма ∑1/ n 3/2ограничена. Заменим для этого 1/ n 3/2площадью прямоугольника с основанием между точками n и n +1 и высотой 1/ n 3/2(рис. 23).
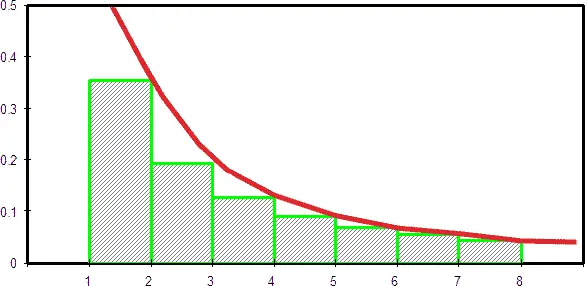
Рис. 23. Доказательство сходимости ряда ∑1/n 3/2
Проведем кривую f ( n ) = 1/( n − 1) 3/2через вершины правых углов прямоугольников.
Площадь под кривой превосходит площадь соответствующих прямоугольников и
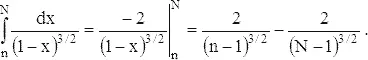
При N → ∞ это выражение стремится к 2( n − 1) 1/2 — конечному пределу. Это показывает, что и предел суммы средних конечен.
Мы можем оценить это число, сложив несколько первых членов ряда 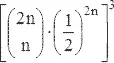 и приблизив «остаток» суммы соответствующим интегралом, что дает приблизительно 0.315. После 10 или, скажем, 20 членов формула Стирлинга очень точна, и остаток, оцениваемый интегралом, весьма мал. Автор при расчете использовал 18 слагаемых. Число 0.315 есть среднее число возвращений частицы в начало координат. Следовательно, 1/ Q = 1 + 0.315, и мы получаем Q = 1/1.315 ≈ 0.761.
и приблизив «остаток» суммы соответствующим интегралом, что дает приблизительно 0.315. После 10 или, скажем, 20 членов формула Стирлинга очень точна, и остаток, оцениваемый интегралом, весьма мал. Автор при расчете использовал 18 слагаемых. Число 0.315 есть среднее число возвращений частицы в начало координат. Следовательно, 1/ Q = 1 + 0.315, и мы получаем Q = 1/1.315 ≈ 0.761.
Поэтому вероятность P того, что частица вернется в начало координат, приблизительно равна 0.239.
Для читателей, знакомых с результатами о случайных блужданиях, где частица сдвигается в центры граней окружающего куба, а не в его вершины, известно, что доля возвращающихся частиц равна приближенно 0.35 [11] В. Феллер, Введение в теорию вероятностей и ее приложения, «Мир», 1964, I т., стр. 353.
, так что для восьми равновероятных шагов шансы на возвращение значительно меньше, чем для шести.
Та же техника в случае 4-мерного блуждания, когда для определения вектора, на который сдвигается частица, бросают четыре монеты, показывает, что вероятность возвращения снижается до 0.105.
53. Решение задачи об игле Бюффона
Это, пожалуй, наиболее известная задача, связанная с геометрическими вероятностями. На рис. 24 показаны положения иглы, при которых она касается одной из прямых. Из соображений симметрии понятно, что достаточно рассмотреть лишь промежуток между какими-нибудь двумя прямыми.
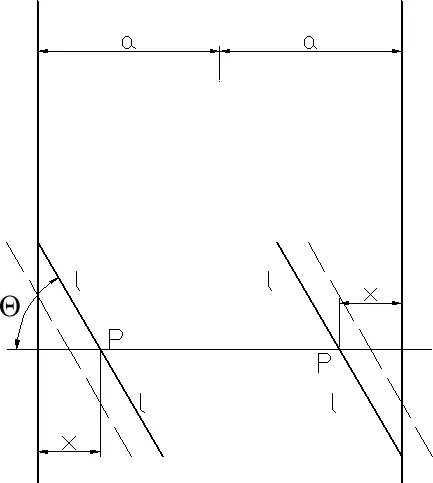
Рис. 24. Иглы, обозначенные пунктиром, пересекают одну из прямых, а проведенные сплошной линией — касаются одной из прямых.
Положение иглы вдоль вертикали не играет здесь никакой роли, так как ее сдвиг вверх или вниз не влияет на пересечение соответствующей прямой. Ясно также, что положение иглы определяется углом между направлением иглы и прямой и расстоянием от центра иглы до ближайшей прямой. Центр P в предположении его равномерного распределения может занять любое положение между прямыми с одинаковой вероятностью, и при фиксированном значении угла θ вероятность того, что игла пересечет одну из прямых, равна 2 x /2 a , так как для пересечения необходимо, чтобы центр иглы упал на расстоянии, меньшем, чем x , от какой-нибудь из прямых (см. рисунок). Мы можем считать, что угол θ равномерно распределен на отрезке от 0 до π/2 (или от 0° до 90°). Действительно, если игла пересекает прямую при угле θ, то это положение вещей сохранится и при угле π − θ (или 180° − θ). Итак, нам надо найти среднее значение величины x / a или, так как x = l ∙cos θ, среднее величины ( l / a )∙cos θ. Это математическое ожидание вычисляется интегрированием
Читать дальшеИнтервал:
Закладка:










