Чарльз Мостеллер - Пятьдесят занимательных вероятностных задач с решениями

Ясно, что других решений у (2) нет. Это может быть доказано методом индукции, так как P (0/ n ) выражается через P (0/1), P (0/2), ..., P (0/ n − 1).

Из (1) и (3), наконец, выводим

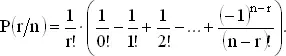
Если n − r велико, то выражение в скобках близко к e −1и

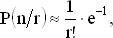
если только n − r достаточно велико. Итак, действительно, вероятности r совпадений в нашей задаче близки к пуассоновским со средним 1. Однако для этой близости необходимо, чтобы разность n − r была велика, а не только само n , как казалось в начале.

Вероятность того, что нет ни одного совпадения, при больших n стремится к e −1≈ 0.368.

Любопытно узнать — на много ли шансы мудреца на успех больше 1/100? Многие предлагают следующую стратегию: пропустить первую половину билетов и затем выбрать первую сумму, превосходящую все предыдущие, если таковая найдется. Это достаточно разумно, но такая стратегия не является оптимальной. Очень немногие представляют себе порядок величины вероятности выигрыша.

Мы начнем с рассмотрения нескольких примеров. Поскольку мы ничего не знаем о суммах, проставленных на билетах, то можем рассматривать лишь номера билетов при их упорядочении согласно величинам сумм, записанных на них. Если, например, у нас имеется три билета с номерами 1, 2, 3, то билету 3 отвечает наибольшее приданое. Для одного или двух билетов задача тривиальна: мудрец делает правильный выбор при одном билете, и его шансы на выигрыш равны 1/2 при двух билетах.

При трех билетах имеем шесть возможных способов вытаскивания:

123 231*

132* 312

213* 321

Одна из стратегий — пропустить первый билет и затем выбрать первый номер, его превосходящий, если такой найдется. Эта стратегия выигрывает в трех случаях, отмеченных звездочкой, т. е. в половине всех возможных случаев, что значительно улучшает просто случайную догадку, например, выбор первого билета.

Допустим теперь, что у нас есть четыре билета. Их возможные перестановки есть

1234 2134 3124*+ 4123

1243+ 2143*+ 3142*+ 4132

1324+ 2314+ 3214*+ 4213

1342+ 2341+ 3241*+ 4231

1423* 2413* 3412* 4312

1432* 2431* 3421* 4321

Кажется разумным пропустить первый билет и остановиться на следующем наибольшем номере, если он есть. Назовем этот план стратегия 1. Звездочки в нашем списке указывают на случай выигрыша этой стратегии. Вероятность правильного решения равна здесь 11/24, что гораздо лучше, чем случайное решение с вероятностью выигрыша 1/4.

Стратегия 2пропускает первые два номера и затем выбирает первый номер, их превосходящий. 10 перестановок, в которых эта стратегия дает выигрыш, отмечены крестиком. Видно, что стратегия 1 выигрывает чаще.

Если продолжать изучение всех возможных случаев их перечислением, то задача приобретает зловещий вид, так как уже для восьми билетов число перестановок есть 40320. Далее, могут существовать хорошие стратегии, которые мы упустим из виду, хотя это кажется невероятным. Будем надеяться, что математика сможет нам помочь.

Следует подчеркнуть, что мудрец ничего не знает о распределении номеров. Чтобы удостовериться в этом, король может сам вытаскивать билеты и сообщать мудрецу их номера среди уже появившихся. Только билет с наибольшим приданым среди вытянутых заслуживает внимания; назовем такое максимальным.

Покажем теперь, что оптимальная стратегия — пропустить s − 1 билетов и выбрать первый максимальный номер после них. Мы выберем максимальное приданое на i -м шагу, если вероятность того, что оно наибольшее среди всех имеющихся, превосходит вероятность правильного решения при оптимальной стратегии и более позднем вытягивании. Формально: остановимся на максимальном номере при i -м вытягивании, если

Р (выиграть при i -м вытягивании) > Р (выиграть при оптимальной стратегии, начиная с i + 1 вытягивания). (1)

Покажем, что вероятность в правой части (1) убывает, когда i возрастает, а вероятность в левой части (1) возрастает с возрастанием i , и потому существует выбор шага i , после которого предпочтительнее удержать максимальное приданое, нежели продолжать испытания. Вычисляя затем вероятность выигрыша для такой стратегии, найдем оптимальный выбор значения s .

После нескольких первых ходов в этой игре мы можем еще прибегнуть ко всем стратегиям, определяемым последующими вытаскиваниями, так как мы всегда можем пропустить часть билетов, пока не достигнем нужного нам числа билетов. Следовательно, вероятность в правой части неравенства (1) не возрастает с ростом i . При i = 0 это искомая оптимальная вероятность, а при i = n − 1 эта вероятность равна 1/ n как вероятность выигрыша при выборе на последнем шагу.

Вероятность того, что на i -м шагу максимальное приданое больше всех имеющихся, равна вероятности того, что наилучший номер находится на одном из первых i билетов, а именно, равна i / n , что является строго возрастающей от 1/ n до 1 функцией от i . Поэтому значение i / n в какой-то точке превосходит вероятность выигрыша при продолжении испытаний. Таким образом, оптимальная стратегия может быть задана следующим правилом: пропустить s − 1 первых номеров и выбрать затем первого лидера, т. е. первый номер, который больше всех предыдущих. Сосчитаем вероятность выигрыша для такой стратегии. Вероятность правильного решения есть вероятность появления ровно одного лидера между s -м шагом и n -м. Вероятность того, что наилучший билет появился на k -м шагу, равна 1/ n . Вероятность того, что максимум первых k − 1 номеров появился среди первых s − 1 номеров, есть ( s − 1)/( k − 1). Произведение ( s − 1)/[ n ·( k − 1)] дает вероятность того, что мы выиграем при выборе k , s ≤ k ≤ n . Суммируя эти числа, получим вероятность π( s , n ) получения наилучшего приданого при оптимальной стратегии

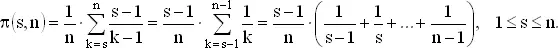(2)

Так как первое вытаскивание всегда дает максимальный номер, то π(1, n) = 1/ n . Заметим, что при n = 4, s = 2 имеем π(1, n ) = 11/24, как и в нашем примере.

Оптимальное значение s , скажем, s *, есть минимальное s , для которого имеет место неравенство (1), т. е. это наименьшее s , для которого

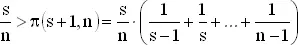(3)