Владимир Живетин - Системы аэромеханического контроля критических состояний

Согласно отмеченному в п. 1, система управления получает на вход с выхода двух систем контроля величины R (1) изм и R (2) изм , отличающиеся на методическую погрешность функционирования систем контроля R м . Система управления обеспечивает R T = R (1) изм и R T = R (2) изм . В первом случае получаем R ф = R Т + (δ R м + δ R и ), во втором – R ф = R Т + δ R и. Величина методической погрешности δ R м , как правило, существенно больше δ R и. По этой причине погрешности управления существующих систем контроля и управления больше.

Для реализации безопасного полета необходимо организовать такое взаимодействие конструкции, обладающей соответствующими характеристиками, и созданного ею ПСАД, при которых выполняется поставленная цель. Особая роль принадлежит подсистеме 3 (рис. 1.5), посредством которой формируется ПСАД для реализации заданной цели на макроуровне, включая: реализацию траектории движения, обеспечение устойчивости, управляемости, реализацию управлений. Структура подсистемы 3 практической реализации цели представлена на рис. 1.7. Здесь обозначено: х доп – допустимое значение х ; x i (3) – заданное значение параметра х i .

Контролю и управлению подлежит совокупность параметров, включающих:

1) параметры, характеризующие цель (например, дальность полета L , высоту полета Н, скорость полета V и т. п.);

2) параметры траектории, с помощью которых задаются области допустимых или безопасных ее состояний (α, V , n y , ω x , ω y , n x, …), где n x , n y – проекции вектора перегрузки на оси ОХ, OY соответственно;

3) параметры траектории полета, используемые при оптимизации эффективности применения техники.

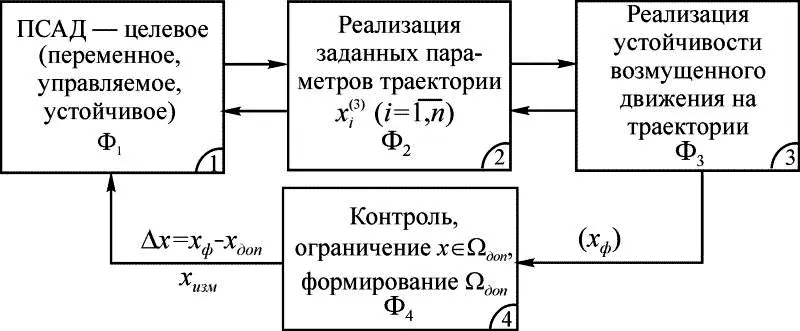
Рис. 1.7

Два основных фактора – поле сил аэродинамического давления и связанный с ним вектор тяги двигателя – задают фактические значения параметров траектории. Проблема контроля над состоянием ЛА связана с контролем над состоянием поля аэродинамического давления на несущих поверхностях, дабы предотвратить:

– разрушение конструкции;

– выход в область критических режимов полета.

Согласно приведенной структуре с функциональными свойствами подсистем Ф 1, Ф 2, Ф 3, Ф 4, для того чтобы аэродинамическая система способна была осуществлять реализацию заданной цели, она должна содержать из области допустимых значений такие показатели, как:

– идентифицируемость (α 1);

– управляемость (α 2);

– наблюдаемость (α 3);

– устойчивость (α 4): устойчивость во внешней среде, т. е. траекторию (α 41); устойчивость во внутренней среде (α 42).

Таким образом, имеют место следующие допустимые множества, порожденные α i α:

Ω доп = Ω доп (α 1,α 2,α 3,α 4);

Ω (1) доп = Ω (1) доп (α 41); Ω (2) доп = Ω (2) доп (α 42); Ω (3) доп = Ω (3) доп (α 43).

При этом имеют место три уровня допустимых состояний аэродинамической системы:

– область допустимых состояний Ω (1) доп есть множество значений х , в которой соблюдается устойчивость фазовых траекторий;

– область Ω (2) доп , в которой соблюдается функциональная устойчивость подсистем аэродинамической системы;

– область Ω доп , в которой реализуется структурная устойчивость аэродинамической системы, обеспечиваемая прежде всего ресурсным потенциалом всех ее подсистем.

Представим области допустимых состояний для аэродинамической системы в явном виде, задав их в виде неравенств.

I. Параметры траектории полета х = ( х 1,…, х 7) включают нижеследующие.

Дальность полета х 1= L ( Т ) ≥ L з , где L з – заданная дальность полета; Т – время полета. При этом L з = L з ( H 3 ,V 3 ,q 3,α 3 ,n 3 y , M 3 ,m 3) ; L ф = L ф ( H ф,V ф,q ф, α ф,… ) – фактическая дальность полета; H ф , V ф , … – фактические значения параметров траектории; H з, V з,… – заданные значения параметров траектории; q – скоростной напор; n з y – заданная величина перегрузки.

Высота полета х 2= Н ф (рис. 1.8): Н 1≤ Н Ф ≤ Н 2, где Н 1 , Н 2 – минимально и максимально допустимые значения высоты полета.

Скорость полета х 3= V ф > V доп .

Скоростной напор 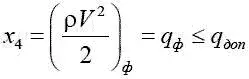, где ρ – плотность воздуха на высоте полета.

Число Маха х 5= М ф ≤ М доп .

Угол атаки крыла х 6= α: α 1≤ α ф ≤ α 2.

Перегрузка x 7= n по вертикальной оси

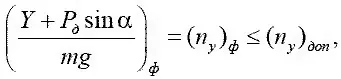
где Y, P р , α – подъемная сила, тяга двигателя, угол атаки соответственно.

В общем случае: α 1, α 2, Н 1 , Н 2 , V доп , q доп , M доп , n у доп – функции таких параметров траектории, как скорость полета V, высота полета Н , число Маха.

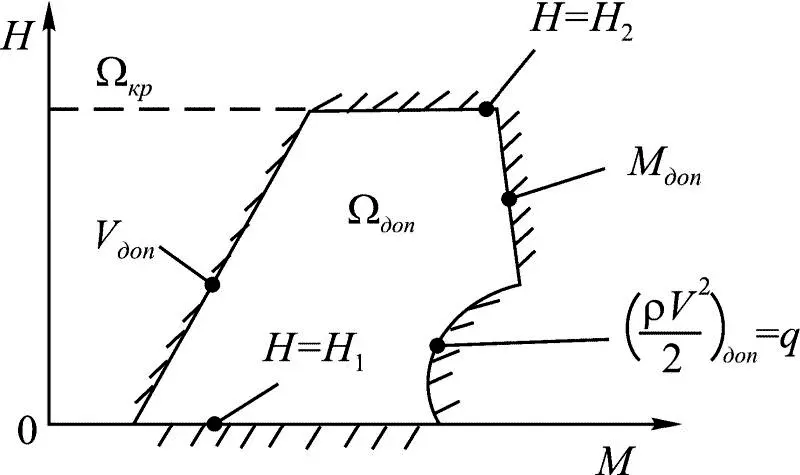
Рис. 1.8

II. Устойчивость возмущенного движения.

Область Ω (1) доп устойчивости возмущенного движения в первом приближении строим, используя линеаризованные уравнения движения вида 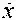= Ах, где А = [ a ij ] nxn – матрица с постоянными элементами а ij . При этом должно соблюдаться неравенство m ij ≤ a ij ≤ M ij , где m ij , M ij зависят от конструктивных параметров аэродинамических поверхностей, создающих ПС АД; a ij = f ( B,X 0), где В – конструктивные параметры самолета, характеризующие его внутренние свойства; Х 0 – начальные значения параметров траектории.

Взаимосвязь а ij и ( B,X 0) устанавливается следующим способом: а ij такое, что γ S < λ 0 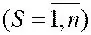, где λ 0 – некоторое заданное отрицательное число, а γ S = Rе λ S ; λ S – корни характеристического уравнения (в общем случае комплексные) для матрицы А, при этом

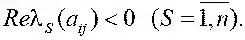
Когда скорость полета возрастает, вещественная часть одного из λ S → 0 и становится при некоторой V кр равной нулю. Тогда самолет становится неустойчив, т. е. покидает область допустимых состояний.