Владимир Живетин - Системы аэромеханического контроля критических состояний

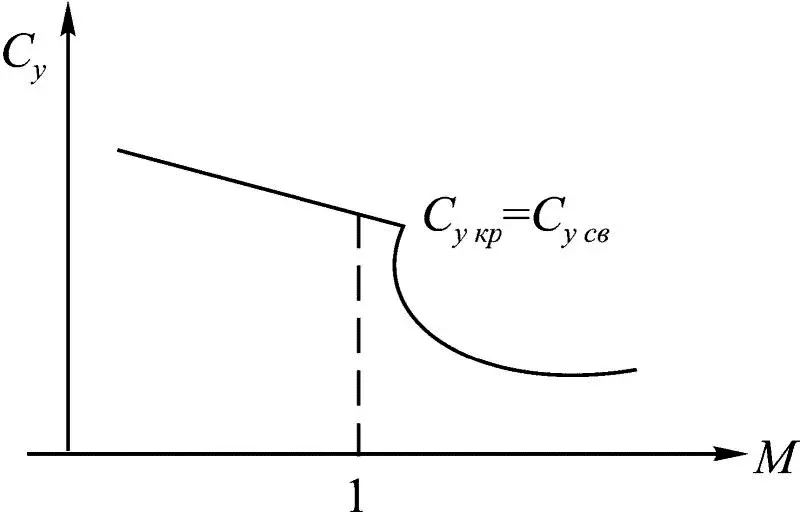
Рис. 1.20

Области допустимых и критических состояний ПСАД, построенных из условий сваливания для различных скоростей полета при выполнении маневров на заданной высоте без вращения и скольжения, изображены на рис. 1.21.

На рис. 1.21 введены обозначения: V св – скорость сваливания; 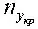– критическое значение перегрузки n у ; V пр – приборная скорость полета; Ω доп , Ω кр – допустимые и критические значения ( V пр , n у ) соответственно.

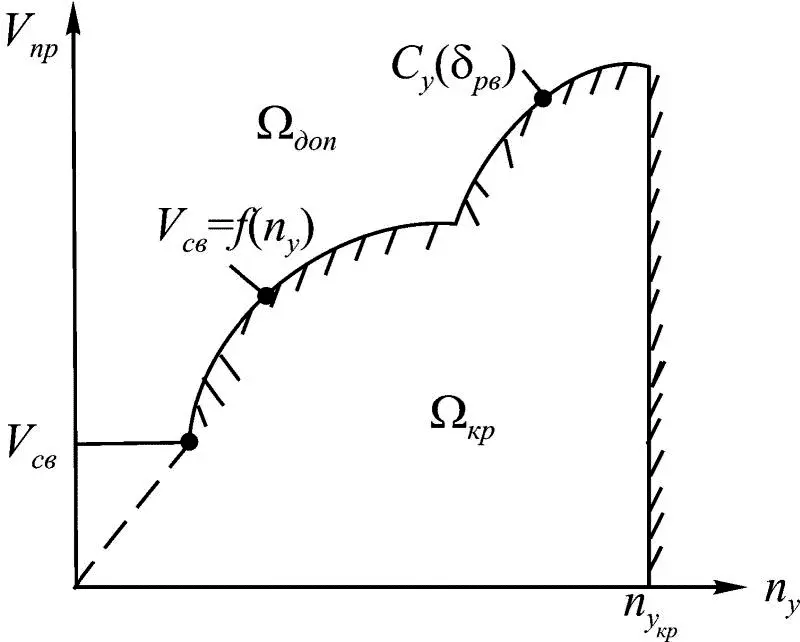
Рис. 1.21

Ситуация существенно изменяется, когда рассматривается ПСАД и его свойства в горизонтальном полете с вращением. При этом область опасных состояний проявляется во взаимодействии продольного и бокового движений, когда создается опасность потери устойчивости, которая зависит (в основном) от следующих факторов: 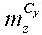– коэффициента продольной статической устойчивости; m β y – коэффициента путевой статической устойчивости; величины угловой скорости ω х ; S – площадь крыла (рис. 1.22). При этом область Ω доп образована огибающими семейства гипербол, являющихся границами областей устойчивости, полученными при различных значениях угловых скоростей вращения самолета.

Расширение коридора обусловлено демпфированием рыскания и тангажа. Всем значениям 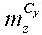и m β y внутри области Ω доп будут соответствовать режимы полета, устойчивые относительно крена при соответствующих ω х .

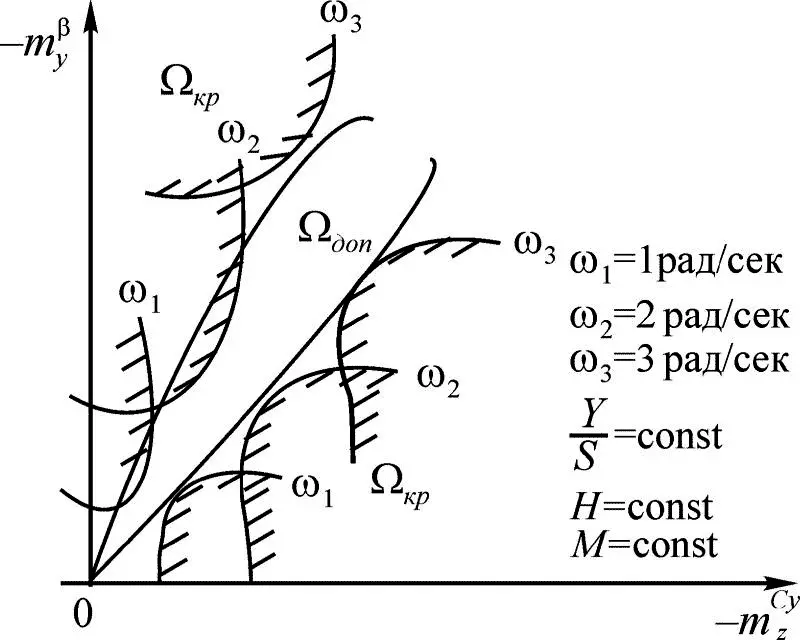
Рис. 1.22

Перекрестные связи между продольным и боковыми моментами сказываются, например, следующим образом: при изменении угла атаки α не только изменяется момент тангажа М z , но и самопроизвольно изменяются моменты рыскания и крена (боковые моменты) и наоборот. Подобные взаимосвязанные изменения характеристик продольного и бокового движений самолета определяются действующими на него аэродинамическими, инерционными и гироскопическими моментами и силами.

Сложность контроля и ограничения параметров фазовой траектории [22] критических значений угловых скорости и ускорения ω x max, ε x max, а также ω y max, ε y maxобусловлено их многозначностью от начальных условий. Так, например, по перегрузке критические значения ω х изменяются от 0,8 рад/сек до 2,0 рад/сек при изменении n у от 1,0 до 2,5 для самолета МиГ-19.

Все сказанное выше позволяет сформулировать

Утверждение.Обеспечение безопасности полета маневренных самолетов целесообразно реализовывать с помощью систем контроля поля сил аэродинамического давления.

В настоящее время одним из альтернативных путей в разработке измерительных систем состояния ЛА в полете является так называемый «активный» аэрометрический метод, в основе которого лежит использование в качестве первичной информации поля аэродинамических давлений на поверхности ЛА, которое определяет реакцию воздушной среды на возмущения, вносимые ЛА. В этом случае как силовое воздействие потока на ЛА и отдельные его части, так и параметры невозмущенного потока могут быть определены косвенным, опосредованным путем через поле давлений на поверхности ЛА, используя при этом законы аэродинамики обтекания, на основе которых и может быть получена адекватная связь между параметрами движения ЛА и точечными характеристиками поля давлений на его поверхности.

Пусть мы имеем возможность контролировать вектор 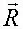как распределенный по поверхности и ограничивать его с помощью соответствующих управлений. Рассмотрим простейшую физическую модель взаимосвязи 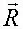с параметрами n у, n x , 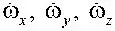при сваливании самолета, когда 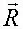принимает значение , контроль над которой мы считаем возможным.

Таким образом, мы рассматриваем плоское движение, когда 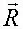= ( R x,R у ), = (( R x ) св ,( R у ) св ), где 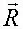– величина аэродинамической силы при отсутствии срыва потока; – величина аэродинамической силы после развития срыва потока. Приращение 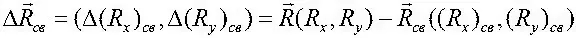обусловливает изменение параметров траектории.

Сила сопротивления R xсв и подъемная сила R усв создают соответствующие перегрузки

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.